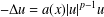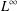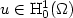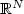7 results
Infinite multiplicity of stable entire solutions for a semilinear elliptic equation with exponential nonlinearity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1371-1404
- Print publication:
- October 2019
-
- Article
- Export citation
TWO-SIDED ESTIMATES FOR POSITIVE SOLUTIONS OF SUPERLINEAR ELLIPTIC BOUNDARY VALUE PROBLEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 30 August 2018, pp. 465-473
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
A Quadratic Triangular Finite Volume Element Method for a Semilinear Elliptic Equation
- Part of
-
- Journal:
- Advances in Applied Mathematics and Mechanics / Volume 9 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 11 October 2016, pp. 186-204
- Print publication:
- February 2017
-
- Article
- Export citation
Schrödinger equations with asymptotically periodic terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 745-757
- Print publication:
- August 2015
-
- Article
- Export citation
Error Estimates for the Numerical Approximationof SemilinearElliptic Control Problemswith Finitely Many State Constraints
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 8 / 2002
- Published online by Cambridge University Press:
- 15 August 2002, pp. 345-374
- Print publication:
- 2002
-
- Article
- Export citation
Sign changing solutions for elliptic equations with critical growth in cylinder type domains
-
- Journal:
- ESAIM: Control, Optimisation and Calculus of Variations / Volume 7 / 2002
- Published online by Cambridge University Press:
- 15 September 2002, pp. 407-419
- Print publication:
- 2002
-
- Article
- Export citation
On positive solutions of some semilinear elliptic equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 343-355
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation