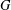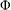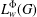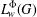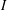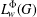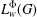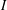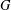For a locally compact group $G$ with left Haar measure and a Young function ${\rm\Phi}$, we define and study the weighted Orlicz algebra $L_{w}^{{\rm\Phi}}(G)$ with respect to convolution. We show that $L_{w}^{{\rm\Phi}}(G)$ admits no bounded approximate identity under certain conditions. We prove that a closed linear subspace $I$ of the algebra $L_{w}^{{\rm\Phi}}(G)$ is an ideal in $L_{w}^{{\rm\Phi}}(G)$ if and only if $I$ is left translation invariant. For an abelian $G$, we describe the spectrum (maximal ideal space) of the weighted Orlicz algebra and show that weighted Orlicz algebras are semisimple.

We prove the semisimplicity conjecture for A-motives over finitely generated fields K. This conjecture states that the rational Tate modules V𝔭(M) of a semisimple A-motive M are semisimple as representations of the absolute Galois group of K. This theorem is in analogy with known results for abelian varieties and Drinfeld modules, and has been sketched previously by Tamagawa. We deduce two consequences of the theorem for the algebraic monodromy groups G𝔭(M) associated to an A-motive M by Tannakian duality. The first requires no semisimplicity condition on M and states that G𝔭(M) may be identified naturally with the Zariski closure of the image of the absolute Galois group of K in the automorphism group of V𝔭(M). The second states that the connected component of G𝔭(M) is reductive if M is semisimple and has a separable endomorphism algebra.

This paper is concerned with rational representations of reductive algebraic groups over fields of positive characteristic $p$. Let $G$ be a simple algebraic group of rank $\ell$. It is shown that a rational representation of $G$ is semisimple provided that its dimension does not exceed $\ell p$. Furthermore, this result is improved by introducing a certain quantity $\mathcal{C}$ which is a quadratic function of $\ell$. Roughly speaking, it is shown that any rational $G$ module of dimension less than $\mathcal{C} p$ is either semisimple or involves a subquotient from a finite list of exceptional modules.

Suppose that $L_1$ and $L_2$ are irreducible representations of $G$. The essential problem is to study the possible extensions between $L_1$ and $L_2$ provided $\dim L_1 + \dim L_2$ is smaller than $\mathcal{C} p$. In this paper, all relevant simple modules $L_i$ are characterized, the restricted Lie algebra cohomology with coefficients in $L_i$ is determined, and the decomposition of the corresponding Weyl modules is analysed. These data are then exploited to obtain the needed control of the extension theory.

1991 Mathematics Subject Classification: 20G05.

In this paper we study categorical compactness with respect to a class of objects F being motiveated by examples arising from modules, abelian groups, and various classes of non-abelian groups. This theory is then applied to the category of not necessarily associative rings. In particular, we study the example arising from the class of all torsion-free rings. This work extends some recent results of B. J. Gardner for associative rings and radical classes.