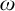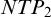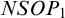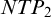4 results
INVARIANT KEISLER MEASURES FOR
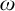 $\omega $-CATEGORICAL STRUCTURES
$\omega $-CATEGORICAL STRUCTURES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERIC EXPANSIONS OF GEOMETRIC THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 18 April 2024, pp. 1-22
-
- Article
-
- You have access
- HTML
- Export citation
La fusion libre : le cas simple
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 7 / Issue 4 / October 2008
- Published online by Cambridge University Press:
- 07 October 2008, pp. 825-868
- Print publication:
- October 2008
-
- Article
- Export citation
Group configurations and germs in simple theories
-
- Journal:
- The Journal of Symbolic Logic / Volume 67 / Issue 4 / December 2002
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1581-1600
- Print publication:
- December 2002
-
- Article
- Export citation