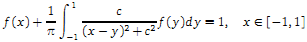Refine search
Actions for selected content:
2 results
17 - Effect of Finite Sampling
-
- Book:
- Time Series Data Analysis in Oceanography
- Published online:
- 21 April 2022
- Print publication:
- 05 May 2022, pp 308-330
-
- Chapter
- Export citation
Sinc Nyström Method for Singularly Perturbed Love's Integral Equation
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 3 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 28 May 2015, pp. 48-58
- Print publication:
- February 2013
-
- Article
- Export citation