We study classes of higher-order singular boundary-value problems on a time scale 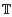 with a positive parameter λ in the differential equations. A homeomorphism and homomorphism ø are involved both in the differential equation and in the boundary conditions. Criteria are obtained for the existence and uniqueness of positive solutions. The dependence of positive solutions on the parameter λ is studied. Applications of our results to special problems are also discussed. Our analysis mainly relies on the mixed monotone operator theory. The results here are new, even in the cases of second-order differential and difference equations.
with a positive parameter λ in the differential equations. A homeomorphism and homomorphism ø are involved both in the differential equation and in the boundary conditions. Criteria are obtained for the existence and uniqueness of positive solutions. The dependence of positive solutions on the parameter λ is studied. Applications of our results to special problems are also discussed. Our analysis mainly relies on the mixed monotone operator theory. The results here are new, even in the cases of second-order differential and difference equations.