1 results
Small G-varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 04 January 2023, pp. 173-215
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
-
An affine variety with an action of a semisimple group G is called “small” if every nontrivial G-orbit in X is isomorphic to the orbit of a highest weight vector. Such a variety X carries a canonical action of the multiplicative group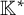
${\mathbb {K}^{*}}$ commuting with the G-action. We show that X is determined by the 
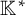${\mathbb {K}^{*}}$-variety 
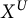$X^U$ of fixed points under a maximal unipotent subgroup 
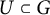$U \subset G$. Moreover, if X is smooth, then X is a G-vector bundle over the algebraic quotient 
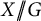$X /\!\!/ G$.If G is of type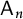
${\mathsf {A}_n}$ (
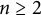$n\geq 2$), 
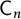${\mathsf {C}_{n}}$, 
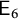${\mathsf {E}_{6}}$, 
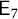${\mathsf {E}_{7}}$, or 
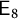${\mathsf {E}_{8}}$, we show that all affine G-varieties up to a certain dimension are small. As a consequence, we have the following result. If 
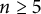$n \geq 5$, every smooth affine 
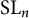$\operatorname {\mathrm {SL}}_n$-variety of dimension 
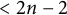$< 2n-2$ is an 
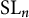$\operatorname {\mathrm {SL}}_n$-vector bundle over the smooth quotient 
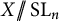$X /\!\!/ \operatorname {\mathrm {SL}}_n$, with fiber isomorphic to the natural representation or its dual.
