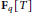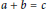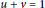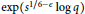1 results
Smooth Polynomial Solutions to a Ternary Additive Equation
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 1 / 01 February 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 117-141
- Print publication:
- 01 February 2018
-
- Article
-
- You have access
- Export citation
-
Let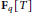
${{\mathbf{F}}_{q}}[T]$ be the ring of polynomials over the finite field of 
$q$ elements and 
$Y$ a large integer. We say a polynomial in 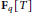${{\mathbf{F}}_{q}}[T]$ is $Y$-smooth if all of its irreducible factors are of degree at most $Y$. We show that a ternary additive equation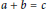 
$a\,+\,b\,=\,c$ over $Y$-smooth polynomials has many solutions. As an application, if 
$S$ is the set of first 
$s$ primes in 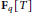${{\mathbf{F}}_{q}}[T]$ and $s$ is large, we prove that the $S$-unit equation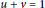 
$u\,+\,v\,=\,1$ has at least 
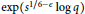$\text{exp}\left( {{s}^{1/6-\in }}\,\text{log}\,\text{q} \right)$ solutions.
