1 results
Weak and classical solutions of equationsof motion for third grade fluids
-
- Journal:
- ESAIM: Mathematical Modelling and Numerical Analysis / Volume 33 / Issue 6 / November 1999
- Published online by Cambridge University Press:
- 15 August 2002, pp. 1091-1120
- Print publication:
- November 1999
-
- Article
- Export citation
-
This paper shows that the decomposition method with special basis, introduced by Cioranescu and Ouazar, allows one to prove global existence in time of the weak solution for the third grade fluids, in three dimensions, with small data. Contrary to the special case where $\vert\alpha_1+\alpha_2\vert\le(24\nu\beta)^{1/2}$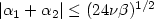
, studied by Amrouche and Cioranescu, the H 1 norm of the velocity is not bounded for all data. This fact, which led others to think, in contradiction to this paper, that the method of decomposition could not apply to the general case of third grade, complicates substantially the proof of the existence of the solution. We also prove further regularity results by a method similar to that of Cioranescu and Girault for second grade fluids. This extension to the third grade fluids is not straightforward, because of a transport equation which is much more complex.
