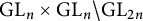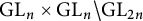1 results
Orbital integrals on
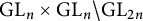 $\text{GL}_n \times \text{GL}_n \backslash \text{GL}_{2n}$
$\text{GL}_n \times \text{GL}_n \backslash \text{GL}_{2n}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 858-886
- Print publication:
- June 2022
-
- Article
- Export citation