We study unitary quotients of the free product unitary pivotal category 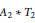${{A}_{2}}\,*\,{{T}_{2}}$. We show that such quotients are parametrized by an integer 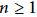$n\,\ge \,1$ and an 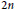$2n$–th root of unity 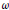$\omega $. We show that for 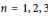$n\,=\,1,\,2,\,3$, there is exactly one quotient and 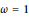$\omega \,=\,1$. For 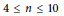$4\,\le \,n\,\le \,10$, we show that there are no such quotients. Our methods also apply to quotients of 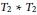${{T}_{2}}\,*\,{{T}_{2}}$, where we have a similar result.

The essence of our method is a consistency check on jellyfish relations. While we only treat the specific cases of 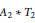${{A}_{2}}\,*\,{{T}_{2}}$ and 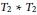${{T}_{2}}\,*\,{{T}_{2}}$, we anticipate that our technique can be extended to a general method for proving the nonexistence of planar algebras with a specified principal graph.

During the preparation of this manuscript, we learnt of Liu's independent result on composites of 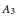${{A}_{3}}$ and 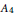${{A}_{4}}$ subfactor planar algebras (arxiv:1308.5691). In 1994, Bisch–Haagerup showed that the principal graph of a composite of 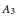${{A}_{3}}$ and 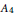${{A}_{4}}$ must fit into a certain family, and Liu has classified all such subfactor planar algebras. We explain the connection between the quotient categories and the corresponding composite subfactor planar algebras. As a corollary of Liu's result, there are no such quotient categories for 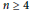$n\,\ge \,4$.

This is an abridged version of arxiv:1308.5723.

The most basic structure of chiral conformal field theory (CFT) is the Verlinde ring. Freed-Hopkins-Teleman have expressed the Verlinde ring for the CFT's associated to loop groups, as twisted equivariant K-theory. We build on their work to express K-theoretically the structures of full CFT. In particular, the modular invariant partition functions (which essentially parametrise the possible full CFTs) have a rich interpretation within von Neumann algebras (subfactors), which has led to the developments of structures of full CFT such as the full system (fusion ring of defect lines), nimrep (cylindrical partition function), alpha-induction etc. Modular categorical interpretations for these have followed. For the generic families of modular invariants (i.e. those associated to Dynkin diagram symmetries), we provide a K-theoretic framework for these other CFT structures, and show how they relate to D-brane charges and charge-groups. 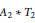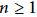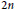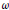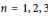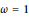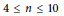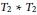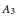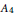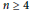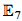We also study conformal embeddings and the modular invariant of SU(2), as well as some families of finite group doubles. This new K-theoretic framework allows us to simplify and extend the less transparent, more ad hoc descriptions of these structures obtained previously within CFT.