We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
For a normalized analytic function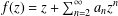 
$f(z)=z+\sum _{n=2}^{\infty }a_{n}z^{n}$ in the unit disk 
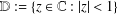$\mathbb{D}:=\{z\in \mathbb{C}:|z|<1\}$, the estimate of the integral means is an important quantity for certain problems in fluid dynamics, especially when the functions 
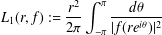$$\begin{eqnarray}L_{1}(r,f):=\frac{r^{2}}{2{\it\pi}}\int _{-{\it\pi}}^{{\it\pi}}\frac{d{\it\theta}}{|f(re^{i{\it\theta}})|^{2}}\end{eqnarray}$$
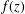$f(z)$ are nonvanishing in the punctured unit disk 
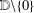$\mathbb{D}\setminus \{0\}$. Let 
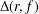${\rm\Delta}(r,f)$ denote the area of the image of the subdisk 
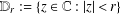$\mathbb{D}_{r}:=\{z\in \mathbb{C}:|z|<r\}$ under 
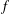$f$, where 
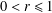$0<r\leq 1$. In this paper, we solve two extremal problems of finding the maximum value of 
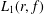$L_{1}(r,f)$ and 
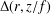${\rm\Delta}(r,z/f)$ as a function of 
$r$ when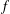 
$f$ belongs to the class of 
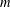$m$-fold symmetric starlike functions of complex order defined by a subordination relation. One of the particular cases of the latter problem includes the solution to a conjecture of Yamashita, which was settled recently by Obradović et al. [‘A proof of Yamashita’s conjecture on area integral’, Comput. Methods Funct. Theory13 (2013), 479–492].
