For a finite group 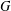 $G$, define
$G$, define 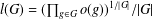 $l(G)=(\prod _{g\in G}o(g))^{1/|G|}/|G|$, where
$l(G)=(\prod _{g\in G}o(g))^{1/|G|}/|G|$, where 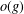 $o(g)$ denotes the order of
$o(g)$ denotes the order of 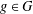 $g\in G$. We prove that if
$g\in G$. We prove that if 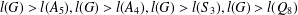 $l(G)>l(A_{5}),l(G)>l(A_{4}),l(G)>l(S_{3}),l(G)>l(Q_{8})$ or
$l(G)>l(A_{5}),l(G)>l(A_{4}),l(G)>l(S_{3}),l(G)>l(Q_{8})$ or 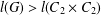 $l(G)>l(C_{2}\times C_{2})$, then
$l(G)>l(C_{2}\times C_{2})$, then 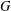 $G$ is solvable, supersolvable, nilpotent, abelian or cyclic, respectively.
$G$ is solvable, supersolvable, nilpotent, abelian or cyclic, respectively.