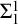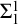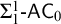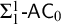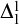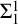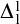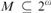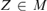Refine search
Actions for selected content:
2 results
THE STRENGTH OF AN AXIOM OF FINITE CHOICE FOR BRANCHES IN TREES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 14 June 2023, pp. 1367-1386
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DETERMINED PROPERTY OF BAIRE IN REVERSE MATH
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 10 September 2019, pp. 166-198
- Print publication:
- March 2020
-
- Article
- Export citation