1 results
CONDITIONAL FEYNMAN INTEGRAL AND SCHRÖDINGER INTEGRAL EQUATION ON A FUNCTION SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 10 March 2009, pp. 1-22
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
-
Let Cr[0,t] be the function space of the vector-valued continuous paths x:[0,t]→ℝr and define Xt:Cr[0,t]→ℝ(n+1)r by Xt(x)=(x(0),x(t1),…,x(tn)), where 0<t1<⋯<tn=t. In this paper, using a simple formula for the conditional expectations of the functions on Cr[0,t] given Xt, we evaluate the conditional analytic Feynman integral Eanfq[Ft∣Xt] of Ft given by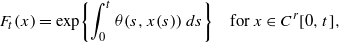
where θ(s,⋅) are the Fourier–Stieltjes transforms of the complex Borel measures on ℝr, and provide an inversion formula for Eanfq[Ft∣Xt]. Then we present an existence theorem for the solution of an integral equation including the integral equation which is formally equivalent to the Schrödinger differential equation. We show that the solution can be expressed by Eanfq[Ft∣Xt] and a probability distribution on ℝr when Xt(x)=(x(0),x(t)).
