2 results
FRAGMENTABILITY BY THE DISCRETE METRIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 2 / April 2015
- Published online by Cambridge University Press:
- 05 January 2015, pp. 303-310
- Print publication:
- April 2015
-
- Article
-
- You have access
- Export citation
-
In a recent paper, topological spaces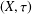
$(X,{\it\tau})$ that are fragmented by a metric that generates the discrete topology were investigated. In the present paper we shall continue this investigation. In particular, we will show, among other things, that such spaces are 
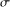${\it\sigma}$-scattered, that is, a countable union of scattered spaces, and characterise the continuous images of separable metrisable spaces by their fragmentability properties.
ON WEAK-FRAGMENTABILITY OF BANACH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 11 June 2014, pp. 251-256
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
