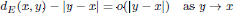1 results
Some new results about the geometry of sets of finite perimeter
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 23 December 2015, pp. 79-105
- Print publication:
- February 2016
-
- Article
- Export citation