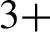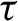We prove by methods of harmonic analysis a result on the existence of solutions for twisted cohomological equations on translation surfaces with loss of derivatives at most 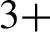 $3+$
in Sobolev spaces. As a consequence we prove that product translation flows on (three-dimensional) translation manifolds which are products of a (higher-genus) translation surface with a (flat) circle are stable in the sense of A. Katok. In turn, our result on product flows implies a stability result of time-
$3+$
in Sobolev spaces. As a consequence we prove that product translation flows on (three-dimensional) translation manifolds which are products of a (higher-genus) translation surface with a (flat) circle are stable in the sense of A. Katok. In turn, our result on product flows implies a stability result of time-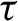 $\tau $
maps of translation flows on translation surfaces.
$\tau $
maps of translation flows on translation surfaces.