1 results
Tree trace reconstruction using subtraces
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 15 December 2022, pp. 629-641
- Print publication:
- June 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
Tree trace reconstruction aims to learn the binary node labels of a tree, given independent samples of the tree passed through an appropriately defined deletion channel. In recent work, Davies, Rácz, and Rashtchian [10] used combinatorial methods to show that
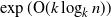$\exp({\mathrm{O}} (k \log_{k} n))$
samples suffice to reconstruct a complete k-ary tree with n nodes with high probability. We provide an alternative proof of this result, which allows us to generalize it to a broader class of tree topologies and deletion models. In our proofs we introduce the notion of a subtrace, which enables us to connect with and generalize recent mean-based complex analytic algorithms for string trace reconstruction.
