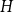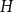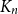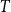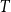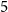A graph 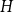 $H$
is common if the number of monochromatic copies of
$H$
is common if the number of monochromatic copies of 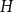 $H$
in a 2-edge-colouring of the complete graph
$H$
in a 2-edge-colouring of the complete graph 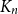 $K_n$
is asymptotically minimised by the random colouring. Burr and Rosta, extending a famous conjecture of Erdős, conjectured that every graph is common. The conjectures of Erdős and of Burr and Rosta were disproved by Thomason and by Sidorenko, respectively, in the late 1980s. Collecting new examples of common graphs had not seen much progress since then, although very recently a few more graphs were verified to be common by the flag algebra method or the recent progress on Sidorenko’s conjecture. Our contribution here is to provide several new classes of tripartite common graphs. The first example is the class of so-called triangle trees, which generalises two theorems by Sidorenko and answers a question of Jagger, Šťovíček, and Thomason from 1996. We also prove that, somewhat surprisingly, given any tree
$K_n$
is asymptotically minimised by the random colouring. Burr and Rosta, extending a famous conjecture of Erdős, conjectured that every graph is common. The conjectures of Erdős and of Burr and Rosta were disproved by Thomason and by Sidorenko, respectively, in the late 1980s. Collecting new examples of common graphs had not seen much progress since then, although very recently a few more graphs were verified to be common by the flag algebra method or the recent progress on Sidorenko’s conjecture. Our contribution here is to provide several new classes of tripartite common graphs. The first example is the class of so-called triangle trees, which generalises two theorems by Sidorenko and answers a question of Jagger, Šťovíček, and Thomason from 1996. We also prove that, somewhat surprisingly, given any tree 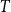 $T$
, there exists a triangle tree such that the graph obtained by adding
$T$
, there exists a triangle tree such that the graph obtained by adding 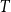 $T$
as a pendant tree is still common. Furthermore, we show that adding arbitrarily many apex vertices to any connected bipartite graph on at most
$T$
as a pendant tree is still common. Furthermore, we show that adding arbitrarily many apex vertices to any connected bipartite graph on at most 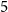 $5$
vertices yields a common graph.
$5$
vertices yields a common graph.