1 results
Triposes as a generalization of localic geometric morphisms
-
- Journal:
- Mathematical Structures in Computer Science / Volume 31 / Issue 9 / October 2021
- Published online by Cambridge University Press:
- 29 January 2021, pp. 1024-1033
-
- Article
- Export citation
-
In Hyland et al. (1980), Hyland, Johnstone and Pitts introduced the notion of tripos for the purpose of organizing the construction of realizability toposes in a way that generalizes the construction of localic toposes from complete Heyting algebras. In Pitts (2002), one finds a generalization of this notion eliminating an unnecessary assumption of Hyland et al. (1980). The aim of this paper is to characterize triposes over a base topos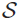
${\cal S}$ in terms of so-called constant objects functors from 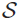${\cal S}$ to some elementary topos. Our characterization is slightly different from the one in Pitts’s PhD Thesis (Pitts, 1981) and motivated by the fibered view of geometric morphisms as described in Streicher (2020). In particular, we discuss the question whether triposes over Set giving rise to equivalent toposes are already equivalent as triposes.
