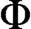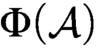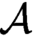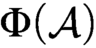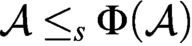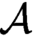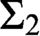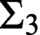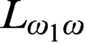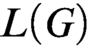Refine search
Actions for selected content:
1 results
CODING IN GRAPHS AND LINEAR ORDERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 18 June 2020, pp. 673-690
- Print publication:
- June 2020
-
- Article
- Export citation