1 results
Parity duality for the amplituhedron
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 09 December 2020, pp. 2207-2262
- Print publication:
- November 2020
-
- Article
- Export citation
-
The (tree) amplituhedron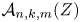
$\mathcal {A}_{n,k,m}(Z)$ is a certain subset of the Grassmannian introduced by Arkani-Hamed and Trnka in 2013 in order to study scattering amplitudes in 
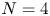$N=4$ supersymmetric Yang–Mills theory. Confirming a conjecture of the first author, we show that when 
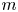$m$ is even, a collection of affine permutations yields a triangulation of 
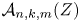$\mathcal {A}_{n,k,m}(Z)$ for any 
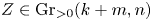$Z\in \operatorname {Gr}_{>0}(k+m,n)$ if and only if the collection of their inverses yields a triangulation of 
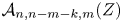$\mathcal {A}_{n,n-m-k,m}(Z)$ for any 
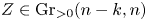$Z\in \operatorname {Gr}_{>0}(n-k,n)$. We prove this duality using the twist map of Marsh and Scott. We also show that this map preserves the canonical differential forms associated with the corresponding positroid cells, and hence obtain a parity duality for amplituhedron differential forms.
