1 results
TWO-SIDED SHIFT SPACES OVER INFINITE ALPHABETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 22 March 2017, pp. 357-386
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
-
Ott, Tomforde and Willis proposed a useful compactification for one-sided shifts over infinite alphabets. Building from their idea, we develop a notion of two-sided shift spaces over infinite alphabets, with an eye towards generalizing a result of Kitchens. As with the one-sided shifts over infinite alphabets, our shift spaces are compact Hausdorff spaces but, in contrast to the one-sided setting, our shift map is continuous everywhere. We show that many of the classical results from symbolic dynamics are still true for our two-sided shift spaces. In particular, while for one-sided shifts the problem about whether or not any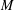
$M$-step shift is conjugate to an edge shift space is open, for two-sided shifts we can give a positive answer for this question.
