1 results
Reciprocal properties of random fields on undirected graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 31 January 2023, pp. 781-796
- Print publication:
- September 2023
-
- Article
-
- You have access
- HTML
- Export citation
-
We clarify and refine the definition of a reciprocal random field on an undirected graph, with the reciprocal chain as a special case, by introducing four new properties: the factorizing, global, local, and pairwise reciprocal properties, in decreasing order of strength, with respect to a set of nodes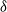
$\delta$. They reduce to the better-known Markov properties if 
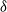$\delta$ is the empty set, or, with the exception of the local property, if 
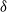$\delta$ is a complete set. Conditions for each reciprocal property to imply the next stronger property are derived, and it is shown that, conditionally on the values at a set of nodes 
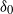$\delta_0$, all four properties are preserved for the subgraph induced by the remaining nodes, with respect to the node set 
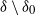$\delta\setminus\delta_0$. We note that many of the above results are new even for reciprocal chains.
