We consider the problem of localizing an inaccessible piece I of the boundary of a conducting medium Ω, and a cavity D contained in Ω, from boundary measurements on the accessible part A of ∂Ω. Assuming that g(t,σ) is the given thermal flux for (t,σ) ∈ (0,T) x A, and that the corresponding output datum is the temperature u(T0,σ) measured at a given time T0 for σ ∈ Aout ⊂ A, we prove that I and D are uniquely localized from knowledge of all possible pairs of input-output data $(g,u(T_0)_{\mid A_{{\rm out}}})$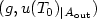. The same result holds when a mean value of the temperature is measured over a small interval of time.