We introduce a new non-abelian quantum synchronisation model over the unitary group, represented as a gradient flow, where state matrices asymptotically converge to a common one up to phase translation. We provide a sufficient framework leading to quantum synchronisation based on Riccati-type differential inequalities. In addition, uniform time-delayed interaction is considered for modelling realistic communication, and we demonstrate that quantum synchronisation is persistent when a small time delay is allowed. Finally, numerical simulation is performed to visualise qualitative behaviours and support theoretical results.

Let F be a field of characteristic two and G a finite abelian 2-group with an involutory automorphism η. If G = H × D with non-trivial subgroups H and D of G such that η inverts the elements of H (H without a direct factor of order 2) and fixes D element-wise, then the linear extension of η to the group algebra FG is called a nice involution. This determines the groups of unitary and symmetric normalized units of FG. We calculate the orders and the invariants of these subgroups.

Inspired by a construction by Bump, Friedberg, and Ginzburg of a two-variable integral representation on $\text{GS}{{\text{p}}_{4}}$ for the product of the standard and spin $L$-functions, we give two similar multivariate integral representations. The first is a three-variable Rankin-Selberg integral for cusp forms on $\text{PG}{{\text{L}}_{4}}$ representing the product of the $L$-functions attached to the three fundamental representations of the Langlands $L$-group $\text{S}{{\text{L}}_{\text{4}}}\left( \text{C} \right)$. The second integral, which is closely related, is a two-variable Rankin-Selberg integral for cusp forms on $\text{PGU}\left( 2,\,2 \right)$ representing the product of the degree $8$ standard $L$-function and the degree $6$ exterior square $L$-function.

Local models are schemes, defined in terms of linear-algebraic moduli problems, which are used to model the étale-local structure of integral models of certain $p$-adic PEL Shimura varieties defined by Rapoport and Zink. In the case of a unitary similitude group whose localization at ${ \mathbb{Q} }_{p} $ is ramified, quasi-split $G{U}_{n} $, Pappas has observed that the original local models are typically not flat, and he and Rapoport have introduced new conditions to the original moduli problem which they conjecture to yield a flat scheme. In a previous paper, we proved that their new local models are topologically flat when $n$ is odd. In the present paper, we prove topological flatness when $n$ is even. Along the way, we characterize the $\mu $-admissible set for certain cocharacters $\mu $ in types $B$ and $D$, and we show that for these cocharacters admissibility can be characterized in a vertexwise way, confirming a conjecture of Pappas and Rapoport.

Following a similar result of Uspenskij on the unitary group of a separable Hilbert space, we show that, with respect to the lower (or Roelcke) uniform structure, the Polish group $G\,=\,\text{Aut(}\mu \text{)}$ of automorphisms of an atomless standard Borel probability space $(X,\,\mu )$ is precompact. We identify the corresponding compactification as the space of Markov operators on ${{L}_{2}}(\mu )$ and deduce that the algebra of right and left uniformly continuous functions, the algebra of weakly almost periodic functions, and the algebra of Hilbert functions on $G$, i.e., functions on $G$ arising from unitary representations, all coincide. Again following Uspenskij, we also conclude that $G$ is totally minimal.

Let K be a CM number field and GK its absolute Galois group. A representation of GK is said to be polarized if it is isomorphic to the contragredient of its outer complex conjugate, up to a twist by a power of the cyclotomic character. Absolutely irreducible polarized representations of GK have a sign ±1, generalizing the fact that a self-dual absolutely irreducible representation is either symplectic or orthogonal. If Π is a regular algebraic, polarized, cuspidal automorphic representation of GLn(𝔸K), and if ρ is a p-adic Galois representation attached to Π, then ρ is polarized and we show that all of its polarized irreducible constituents have sign +1 . In particular, we determine the orthogonal/symplectic alternative for the Galois representations associated to the regular algebraic, essentially self-dual, cuspidal automorphic representations of GLn (𝔸F) when F is a totally real number field.

We continue our study of the reduction of PEL Shimura varieties with parahoric level structure at primes p at which the group defining the Shimura variety ramifies. We describe ‘good’ p-adic integral models of these Shimura varieties and study their étale local structure. In the present paper we mainly concentrate on the case of unitary groups for a ramified quadratic extension. Some of our results are applications of the theory of twisted affine flag varieties that we developed in a previous paper.

we study some automorphic cohomology classes of degree one on the griffiths–schmid varieties attached to some unitary groups in three variables. using partial compactifications of those varieties, constructed by kato and usui, we define for such a cohomology class some analogues of fourier–shimura coefficients, which are cohomology classes on certain elliptic curves. we show that a large space of such automorphic classes can be generated by those with rational ‘coefficients’. more precisely, we consider those cohomology classes that come from picard modular forms, via some penrose-like transform studied in a previous article: we prove that the coefficients of the classes thus obtained can be computed from the coefficients of the picard form by a similar transform defined at the level of the elliptic curve.

Let $\mathcal{M}$ be a type $\text{I}{{\text{I}}_{1}}$ von Neumann algebra, $\tau$ a trace in $\mathcal{M}$, and ${{L}^{2}}\left( \mathcal{M},\tau \right)$ the GNS Hilbert space of $\tau$. We regard the unitary group ${{U}_{\mathcal{M}}}$ as a subset of ${{L}^{2}}\left( \mathcal{M},\tau \right)$ and characterize the shortest smooth curves joining two fixed unitaries in the ${{L}^{2}}$ metric. As a consequence of this we obtain that ${{U}_{\mathcal{M}}}$, though a complete (metric) topological group, is not an embedded riemannian submanifold of ${{L}^{2}}\left( \mathcal{M},\tau \right)$

Let 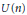$U(n)$ be the group of 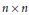$n\,\times \,n$ unitary matrices. We show that if 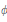$\phi $ is a linear transformation sending 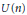$U(n)$ into 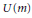$U(m)$, then 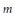$m$ is a multiple of 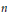$n$, and 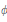$\phi $ has the form

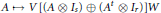$$A\,\mapsto \,V[(A\,\otimes \,{{I}_{s}})\,\otimes \,({{A}^{t}}\,\otimes \,{{I}_{r}})]W$$

for some 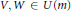$V,\,W\,\in \,U(m)$. From this result, one easily deduces the characterization of linear operators that map 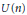$U(n)$ into itself obtained by Marcus. Further generalization of the main theorem is also discussed.