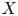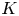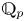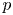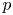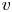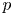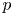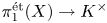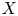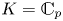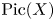1 results
A geometric p-adic Simpson correspondence in rank one
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 21 May 2024, pp. 1433-1466
- Print publication:
- July 2024
-
- Article
- Export citation