Let 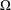 $\unicode[STIX]{x1D6FA}$ be a domain in
$\unicode[STIX]{x1D6FA}$ be a domain in 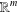 $\mathbb{R}^{m}$ with nonempty boundary. In Ward [‘On essential self-adjointness, confining potentials and the
$\mathbb{R}^{m}$ with nonempty boundary. In Ward [‘On essential self-adjointness, confining potentials and the 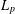 $L_{p}$-Hardy inequality’, PhD Thesis, NZIAS Massey University, New Zealand, 2014] and [‘The essential self-adjointness of Schrödinger operators on domains with non-empty boundary’, Manuscripta Math.150(3) (2016), 357–370] it was shown that the Schrödinger operator
$L_{p}$-Hardy inequality’, PhD Thesis, NZIAS Massey University, New Zealand, 2014] and [‘The essential self-adjointness of Schrödinger operators on domains with non-empty boundary’, Manuscripta Math.150(3) (2016), 357–370] it was shown that the Schrödinger operator 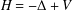 $H=-\unicode[STIX]{x1D6E5}+V$, with domain of definition
$H=-\unicode[STIX]{x1D6E5}+V$, with domain of definition 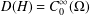 $D(H)=C_{0}^{\infty }(\unicode[STIX]{x1D6FA})$ and
$D(H)=C_{0}^{\infty }(\unicode[STIX]{x1D6FA})$ and 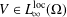 $V\in L_{\infty }^{\text{loc}}(\unicode[STIX]{x1D6FA})$, is essentially self-adjoint provided that
$V\in L_{\infty }^{\text{loc}}(\unicode[STIX]{x1D6FA})$, is essentially self-adjoint provided that 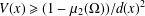 $V(x)\geq (1-\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA}))/d(x)^{2}$. Here
$V(x)\geq (1-\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA}))/d(x)^{2}$. Here 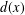 $d(x)$ is the Euclidean distance to the boundary and
$d(x)$ is the Euclidean distance to the boundary and  $\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA})$ is the nonnegative constant associated to the
$\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA})$ is the nonnegative constant associated to the 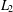 $L_{2}$-Hardy inequality. The conditions required for a domain to admit an
$L_{2}$-Hardy inequality. The conditions required for a domain to admit an 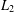 $L_{2}$-Hardy inequality are well known and depend intimately on the Hausdorff or Aikawa/Assouad dimension of the boundary. However, there are only a handful of domains where the value of
$L_{2}$-Hardy inequality are well known and depend intimately on the Hausdorff or Aikawa/Assouad dimension of the boundary. However, there are only a handful of domains where the value of 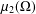 $\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA})$ is known explicitly. By obtaining upper and lower bounds on the number of cubes appearing in the
$\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6FA})$ is known explicitly. By obtaining upper and lower bounds on the number of cubes appearing in the  $k\text{th}$ generation of the Whitney decomposition of
$k\text{th}$ generation of the Whitney decomposition of  $\unicode[STIX]{x1D6FA}$, we derive an upper bound on
$\unicode[STIX]{x1D6FA}$, we derive an upper bound on 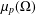 $\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x1D6FA})$, for
$\unicode[STIX]{x1D707}_{p}(\unicode[STIX]{x1D6FA})$, for 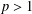 $p>1$, in terms of the inner Minkowski dimension of the boundary.
$p>1$, in terms of the inner Minkowski dimension of the boundary.
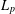 $L_{p}$-HARDY INEQUALITY
$L_{p}$-HARDY INEQUALITY