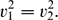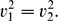2 results
Stability of weakly dissipative Reissner–Mindlin–Timoshenko plates: A sharp result
-
- Journal:
- European Journal of Applied Mathematics / Volume 29 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 27 April 2017, pp. 226-252
-
- Article
- Export citation
-
In the present article, we show that there exists a critical number that stabilizes the Reissner–Mindlin–Timoshenko system with frictional dissipation acting on rotation angles. We identify two speed characteristics v12:=K/ρ1 and v22:=D/ρ2, and we show that the system is exponentially stable if and only if
For v12 ≠ v22, we prove that the system is polynomially stable and determine an optimal estimate for the decay. To confirm our analytical results, we compute the numerical solutions by means of several numerical experiments by using a finite difference method.
\begin{equation*}
v_{1}^{2}=v_{2}^{2}.
\end{equation*}
Stability to the dissipative Reissner–Mindlin–Timoshenko acting on displacement equation†
-
- Journal:
- European Journal of Applied Mathematics / Volume 27 / Issue 2 / April 2016
- Published online by Cambridge University Press:
- 26 August 2015, pp. 157-193
-
- Article
- Export citation
-
In this paper, we show that there exists a critical number that stabilises the Reissner–Mindlin–Timoshenko system with frictional dissipation acting only on the equation for the transverse displacement. We identify that the Reissner–Mindlin–Timoshenko system has two speed characteristics v12 := K/ρ1 and v22 := D/ρ2 and we show that the system is exponentially stable if only if
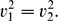\begin{equation*}
v_{1}^{2}=v_{2}^{2}.
\end{equation*}In the general case, we prove that the system is polynomially stable with optimal decay rate. Numerical experiments using finite differences are given to confirm our analytical results. Our numerical results are qualitatively in agreement with the corresponding results from dynamical in infinite dimensional.
