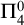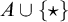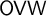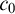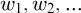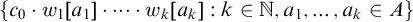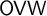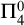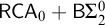Refine search
Actions for selected content:
4 results
Papers on weak first-order theories and decidability problems
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 15 December 2025, p. 696
- Print publication:
- December 2025
-
- Article
-
- You have access
- Export citation
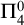 $\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
$\Pi ^0_4$ CONSERVATION OF THE ORDERED VARIABLE WORD THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-16
-
- Article
- Export citation
A PARAMETERIZED HALTING PROBLEM,
 $ \Delta _0$ TRUTH AND THE MRDP THEOREM
$ \Delta _0$ TRUTH AND THE MRDP THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 September 2024, pp. 483-508
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
END-EXTENSIONS OF MODELS OF WEAK ARITHMETIC FROM COMPLEXITY-THEORETIC CONTAINMENTS
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 19 July 2016, pp. 901-916
- Print publication:
- September 2016
-
- Article
- Export citation