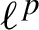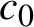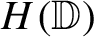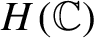Refine search
Actions for selected content:
4 results
Zero-one law of orbital limit points for weighted shifts
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 945-978
-
- Article
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chaos and frequent hypercyclicity for weighted shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 3634-3670
- Print publication:
- December 2021
-
- Article
- Export citation
L(n)-HYPONORMALITY: A MISSING BRIDGE BETWEEN SUBNORMALITY AND PARANORMALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 01 April 2010, pp. 193-203
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation