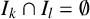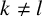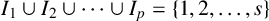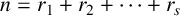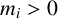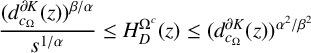ON THE GENERALISED SQUEEZING FUNCTION

Abstract

In this article, we clarify the relation between the squeezing function and the Fridman invariant corresponding to a general domain $\Omega $ (not necessarily convex), where $\Omega $ is defined by

$$ \begin{align*}\Omega = \bigg\lbrace z \in \mathbb{C}^{r_{1}}\times\mathbb{C}^{r_{2}}\times\cdots\times\mathbb{C}^{r_{s}} : \sum\limits_{i\in I_{k}} ||z_{i}||^{m_{i}} < 1, 1\leq k \leq p \bigg\rbrace,\end{align*} $$

with $I_{k}\cap I_{l} = \emptyset $ if $k\neq l$, $I_{1}\cup I_{2} \cup \cdots \cup I_{p} = \lbrace 1, 2, \ldots , s\rbrace $, $n = r_{1} + r_{2} + \cdots + r_{s}$ and $m_{i}> 0$ for all i. Furthermore, we give an example of a domain whose squeezing function corresponding to $\Omega $ is not plurisubharmonic.

1 Introduction

Nonavailability of the Riemann mapping theorem in $\mathbb {C}^{n}\ (n\geq 2)$ makes the study of biholomorphic equivalence of different domains an interesting and important activity. This leads to different types of holomorphic invariants to establish analytic and geometric properties of bounded domains. The squeezing function is one such holomorphic invariant, which has been intensively studied in the last few years. In 2012, Deng et al. [2] introduced the squeezing function $S_{\Omega }$ by building on the work of Liu et al. [11, 12] and Yeung [16].

Let $D\subseteq \mathbb {C}^n$ be a bounded domain. For $z\in D$ and an injective holomorphic mapping $f:D\to \mathbb {B}^n$ with $f(z)=0$ , define

$$ \begin{align*}S_{D}(z,f) = \sup \{r:\mathbb{B}^n(0,r)\subseteq f(D)\},\end{align*} $$

where $\mathbb {B}^n$ denotes the unit ball in $\mathbb {C}^n$ and $\mathbb {B}^n(0,r)$ denotes the ball centred at the origin with radius r in $\mathbb {C}^n$ . The squeezing function on D, denoted by $S_{D}$ , is defined by

$$ \begin{align*}S_{D}(z) = \sup_f\{S_{D}(z,f)\},\end{align*} $$

where the supremum is taken over all injective holomorphic mappings $f:D\to \mathbb {B}^n$ with $f(z)=0.$

Fornæss, in his talk [3], posed the question, ‘What is the analogous theory of the squeezing function when the model domain is changed to the unit polydisc instead of the unit ball?’ Considering this question, Gupta and Pant [7] introduced the squeezing function corresponding to the polydisc by taking injective holomorphic mappings into the unit polydisc and discussed some of its properties.

Rong and Yang [14] introduced the generalised squeezing function by taking injective holomorphic mappings into a bounded, balanced and convex domain in $\mathbb {C}^{n}$ . The definition uses the Minkowski function for balanced domains. The Minkowski function for the balanced domain $\Omega $ , denoted by $\rho _{\Omega }$ , is defined by

$$ \begin{align*}\rho_{\Omega}(z) = \inf \lbrace t> 0 : z/t\in \Omega\rbrace,\quad z\in \mathbb{C}^{n}. \end{align*} $$

Gupta and Pant [8] introduced the d-balanced squeezing function by taking injective holomorphic mappings into a bounded, d-balanced and convex domain in $\mathbb {C}^{n}$ . They used the d-Minkowski function to define their squeezing function.

Motivated by this work, Chrih and Khelifi [1] introduced the squeezing function corresponding to a general domain $\Omega \subseteq \mathbb {C}^{n}$ defined by

(1.1) $$ \begin{align} \Omega = \bigg\lbrace z \in \mathbb{C}^{r_{1}}\times\mathbb{C}^{r_{2}}\times\cdots\times\mathbb{C}^{r_{s}} : \sum\limits_{i\in I_{k}} ||z_{i}||^{m_{i}} < 1, 1\leq k \leq p \bigg\rbrace, \end{align} $$

with $I_{k}\cap I_{l} = \emptyset $ if $k\neq l$ , $I_{1}\cup I_{2} \cup \cdots \cup I_{p} = \lbrace 1, 2, \ldots , s\rbrace $ , $n = r_{1} + r_{2} + \cdots + r_{s}$ and $m_{i}> 0$ for all i.

Note that $\Omega $ is bounded, balanced, but not necessarily convex and provides a concrete model space with which to work. Observe that the unit ball and the unit polydisc are special cases of $\Omega $ . The definition of the squeezing function corresponding to the general domain $\Omega $ is formulated as follows.

Let $D\subseteq \mathbb {C}^n$ be a bounded domain. For $z\in D$ and an injective holomorphic mapping $f:D\to \Omega $ with $f(z)=0$ , define

$$ \begin{align*}S_{D}^{\Omega}(z,f) = \sup \{r: \Omega(r)\subseteq f(D)\},\end{align*} $$

where

$$ \begin{align*}\Omega(r) = \bigg\lbrace z \in \mathbb{C}^{r_{1}}\times\mathbb{C}^{r_{2}}\times\cdots\times\mathbb{C}^{r_{s}} : \sum\limits_{i\in I_{k}} ||z_{i}||^{m_{i}} < r, 1\leq k \leq p \bigg\rbrace.\end{align*} $$

The squeezing function corresponding to $\Omega $ on D, denoted by $S_{D}^{\Omega }$ , is defined by

$$ \begin{align*}S_{D}^{\Omega}(z) = \sup_f\{S_{D}^{\Omega}(z,f)\},\end{align*} $$

where the supremum is taken over all injective holomorphic mappings $f:D\to \Omega $ with $f(z)=0$ . For many interesting properties of $S_{D}^{\Omega }$ , we refer to [1].

The Fridman invariant is another holomorphic invariant of bounded domains, introduced by Fridman in [5]. Let $D\subseteq \mathbb {C}^n$ be a bounded domain and $\Omega \subseteq \mathbb {C}^n$ a bounded homogeneous domain. For $z\in D$ , the Fridman invariant, denoted by $h_{D}^{\Omega ^{d}}$ , is defined by

$$ \begin{align*}h_{D}^{\Omega^{d}}(z)= \inf\bigg\lbrace \dfrac{1}{r} : B_{D}^{d}(z, r)\subseteq f(\Omega), f: \Omega \to D \bigg\rbrace,\end{align*} $$

where $f:\Omega \to D$ is an injective holomorphic mapping and $B_{D}^{d}(z, r)$ is a ball centred at z with radius r with respect to the d-metric (which is either the Carathéodory metric or the Kobayashi metric). Nikolov and Verma [13] considered a modification of $h_{D}^{\Omega ^{d}}$ , which is denoted by $H_{D}^{\Omega ^{d}}$ and defined by

$$ \begin{align*}H_{D}^{\Omega^{d}}(z) = \sup \lbrace \tanh r : B_{D}^{d}(z, r) \subseteq f(\Omega), f:\Omega\to D \rbrace,\end{align*} $$

where $f:\Omega \to D$ is an injective holomorphic mapping. In [13], Nikolov and Verma gave a relation between the squeezing function and the Fridman invariant:

(1.2) $$ \begin{align} S_{D}(z) \leq H_{D}^{c}(z) \leq H_{D}^{k}(z), \quad z\in D, \end{align} $$

where $H_{D}^{c}(z)$ and $H_{D}^{k}(z)$ denote the Fridman invariant for $\Omega = \mathbb {B}^{n}$ with respect to the Carathéodory metric and Kobayashi metric, respectively. In [15], Rong and Yang proved that this relation holds for generalised squeezing functions.

In Theorem 2.1 of this article, we find the analogous result to (1.2) for the squeezing function $S_{D}^{\Omega }$ , where $\Omega $ is given in (1.1). In Theorem 2.3, we give some lower and upper bound estimates for the squeezing function $S_{D}^{\Omega }$ of some special domains which are analogous to [15, Theorem 2.1]. In Theorem 2.8, we give some lower and upper bound estimates for the Fridman invariant $H_{D}^{\Omega }$ .

In [4], Fornæss and Scherbina gave an example of a domain for which the squeezing function corresponding to the unit ball is nonplurisubharmonic. Rong and Yang in [15] gave examples of domains for which the generalised squeezing function is nonplurisubharmonic. Motivated by their work, Gupta and Pant in [6] gave an example of a domain for which the d-balanced squeezing function is nonplurisubharmonic.

In Theorem 3.1, we give an example of a domain $D$ for which $S_{D}^{\Omega }$ is nonplurisubharmonic.

2 ${\mathit {S}_{\mathit {D}}^{\Omega }}$ and ${\mathit {H}_{\mathit {D}}^{\Omega }}$

Let us fix some notation. We denote the unit polydisc in $\mathbb {C}^{n}$ by $\mathbb {D}^{n}$ , and the polydisc with centre zero and radius r in $\mathbb {C}^{n}$ by $\mathbb {D}^{n}(0, r)$ . Let $D \subseteq \mathbb {C}^{n}$ be a domain. The Carathéodory pseudo-distance between $z_{1}, z_{2}\in D$ , denoted by $c_{D}(z_{1}, z_{2})$ , is

$$ \begin{align*}c_{D}(z_{1}, z_{2}) = \displaystyle\sup_{f}\lbrace \tanh^{-1}|p| : f:D\to \mathbb{D}\ \text{holomorphic}, f(z_{1})=0, f(z_{2})= p \rbrace.\end{align*} $$

For $z = (z_{1}, z_{2},\ldots , z_{n}), a = (a_{1}, a_{2},\ldots , a_{n})\in \mathbb {D}^{n}$ ,

(2.1) $$ \begin{align} \tanh c_{\mathbb{D}^{n}}(z, a) = \max_{1 \leq i \leq n}\bigg|\dfrac{z_{i}-a_{i}}{1-\overline{a}_{i}z_{i}}\bigg|. \end{align} $$

For a real number $\lambda> 0$ ,

$$ \begin{align*} \Omega^{\lambda} = \bigg\lbrace z \in \mathbb{C}^{r_{1}}\times\mathbb{C}^{r_{2}}\times\cdots\times\mathbb{C}^{r_{s}} : \sum\limits_{i\in I_{k}} ||z_{i}||^{\lambda} < 1, 1\leq k \leq p \bigg\rbrace, \end{align*} $$

where $I_{k}\cap I_{l} = \emptyset $ if $k\neq l$ , $I_{1}\cup I_{2} \cup \cdots \cup I_{p} = \lbrace 1, 2, \ldots , s\rbrace $ , $n = r_{1} + r_{2} + \cdots + r_{s}$ and

$$ \begin{align*} \Omega^{\lambda}(r) = \bigg\lbrace z \in \mathbb{C}^{r_{1}}\times\mathbb{C}^{r_{2}}\times\cdots\times\mathbb{C}^{r_{s}} : \sum\limits_{i\in I_{k}} ||z_{i}||^{\lambda} < r, 1\leq k \leq p \bigg\rbrace. \end{align*} $$

Let $\alpha = \min _{i}{m_{i}}$ and $\beta = \max _{i}{m_{i}}$ , where the $m_{i}> 0$ are given in (1.1). If $m_{i} \geq 1$ for all i, then by [9, Proposition 2.3.1(c)], it is easy to see that

(2.2) $$ \begin{align} \bigg(\sum\limits_{i\in I_{k}}||z_{i}||^{m_{i}}\bigg)^{1/\alpha} \leq \tanh c_{\Omega}(0, z) \leq \bigg(\sum\limits_{i\in I_{k}}||z_{i}||^{m_{i}}\bigg)^{1/\beta} \end{align} $$

for $z = (z_{1}, z_{2},\ldots , z_{s})\in \Omega $ and $1 \leq k \leq p$ . Note that by [9, Proposition 2.3.1(a)], the right-hand inequality (2.2) holds for all $m_{i}> 0$ . If K is a compact subset of $\Omega $ such that $\Omega \setminus K$ is connected, then

$$ \begin{align*}d_{c_{\Omega}}^{K}(z) = \min_{w\in K} \tanh [c_{\Omega}(z, w)], \quad z\in\Omega\setminus K.\end{align*} $$

Theorem 2.1. Let D be a bounded domain in $\mathbb {C}^{n}$ and $\Omega $ in (1.1) be homogeneous. Then:

1. (1) $(S_{D}^{\Omega }(z))^{\beta /\alpha ^{2}} \leq H_{D}^{\Omega ^{c}}(z) \leq H_{D}^{\Omega ^{k}}(z)$ for $z\in D$ if all $m_{i} \geq 1$ ;

2. (2) $({S_{D}^{\Omega }(z)}/{s})^{1/\alpha } \leq H_{D}^{\Omega ^{c}}(z) \leq H_{D}^{\Omega ^{k}}(z)$ for $z\in D$ if at least one $m_{i} < 1$ .

Proof. For part (1), since $c_{D}\leq k_{D}$ , it follows that $H_{D}^{\Omega ^{c}}(z) \leq H_{D}^{\Omega ^{k}}(z)$ for all $z\in D$ . To prove the first inequality, let us assume that $S_{D}^{\Omega }(z) = r> 0$ for some $z\in D$ . By [1, Theorem 2.5], there exists an injective holomorphic mapping $f : D \to \Omega $ such that $f(z) = 0$ and $\Omega (r) \subseteq f(D) \subseteq \Omega $ .

Consider the injective holomorphic mapping $g : \Omega \to \mathbb {C}^{n}$ given by $g(\xi ) = r^{1/\alpha }\xi $ . Let $w = (w_{1}, w_{2},\ldots , w_{s})\in \Omega $ and $g(w) = (w_{1}', w_{2}',\ldots , w_{s}') $ . Then,

$$ \begin{align*}\sum\limits_{i\in I_{k}}||w_{i}'||^{m_{i}} = \sum\limits_{i\in I_{k}}||r^{1/\alpha}w_{i}||^{m_{i}} \leq r\sum\limits_{i\in I_{k}} ||w_{i}||^{m_{i}} < r\end{align*} $$

for $1 \leq k \leq p$ . This implies that $g(\Omega ) \subseteq \Omega (r)$ . Therefore, $h = (f^{-1}\circ g) : \Omega \to D$ is an injective holomorphic mapping with $h(0)= z$ .

We claim that $B_{D}^{c}(z, \tanh ^{-1}r^{\beta /\alpha ^{2}}) \subseteq h(\Omega )$ . To prove our claim, consider $w = (w_{1}, w_{2},\ldots , w_{n})\in B_{D}^{c}(z, \tanh ^{-1}r^{\beta /\alpha ^{2}})$ and $f(w) = (w_{1}', w_{2}',\ldots , w_{s}') $ . By (2.2),

(2.3) $$ \begin{align} r^{\beta/\alpha^{2}}> \tanh c_{D}(z, w) \geq \tanh c_{\Omega}(0, f(w)) \geq \bigg(\sum\limits_{i\in I_{k}}||w_{i}'||^{m_{i}}\bigg)^{1/\alpha} \end{align} $$

for $1 \leq k \leq p$ . Let $a = ({w_{1}'}/{r^{1/\alpha }}, {w_{2}'}/{r^{1/\alpha }},\ldots , {w_{s}'}/{r^{1/\alpha }})$ . By (2.3),

$$ \begin{align*} \sum\limits_{i\in I_{k}}\bigg\|\dfrac{w_{i}'}{r^{1/\alpha}}\bigg\|^{m_{i}} \leq \sum\limits_{i\in I_{k}} \dfrac{||w_{i}'||^{m_{i}}}{r^{\beta/\alpha}} < 1 \end{align*} $$

for $1 \leq k \leq p$ . It follows that $a\in \Omega $ with $h(a) = w$ . Therefore, $w \in h(\Omega )$ , which proves our claim. Hence, if all $m_{i} \geq 1$ ,

$$ \begin{align*}(S_{D}^{\Omega}(z))^{\beta/\alpha^{2}} \leq H_{D}^{\Omega^{c}}(z) \leq H_{D}^{\Omega^{k}}(z),\quad z\in D.\end{align*} $$

For part (2), assume that $m_{i} \geq 1$ for some i. Proceeding as in part (1), we claim that $B_{D}^{c}(z, \tanh ^{-1}({r}/{s})^{1/\alpha }) \subseteq h(\Omega )$ . Observe that $\Omega \subseteq \Omega ^{\beta }$ and therefore,

(2.4) $$ \begin{align} \tanh c_{\Omega^{\beta}}(0, \xi) \leq \tanh c_{\Omega}(0, \xi)\quad \text{for all}\ \xi\in \Omega. \end{align} $$

To prove our claim, consider $w = (w_{1}, w_{2},\ldots , w_{n})\in B_{D}^{c}(z, \tanh ^{-1}({r}/{s})^{1/\alpha })$ and $f(w) = (w_{1}', w_{2}',\ldots , w_{s}') $ . By (2.2) and (2.4),

(2.5) $$ \begin{align} \bigg(\dfrac{r}{s}\bigg)^{1/\alpha}> \tanh c_{D}(z, w) \geq \tanh c_{\Omega^{\beta}}(0, f(w)) = \bigg(\sum\limits_{i\in I_{k}}||w_{i}'||^{\beta}\bigg)^{1/\beta} \end{align} $$

for $1 \leq k \leq p$ . Let $a = ({w_{1}'}/{r^{1/\alpha }}, {w_{2}'}/{r^{1/\alpha }},\ldots , {w_{s}'}/{r^{1/\alpha }})$ . By (2.5),

$$ \begin{align*} \sum\limits_{i\in I_{k}}\bigg\|\dfrac{w_{i}'}{r^{1/\alpha}}\bigg\|^{\beta} \leq \sum\limits_{i\in I_{k}} \dfrac{||w_{i}'||^{\beta}}{r^{\beta/\alpha}} < \dfrac{1}{s^{\beta/\alpha}} \end{align*} $$

for $1 \leq k \leq p$ . It follows that $a\in \Omega ^{\beta }({1}/{s^{\beta /\alpha }})$ . It is easy to see that $\Omega ^{\beta }({1}/{s^{\beta /\alpha }})\subseteq \Omega $ . Therefore, $a\in \Omega $ with $h(a) = w$ , which proves our claim. If all $m_{i} < 1$ , take $\beta = 1$ in the above argument and the proof follows the same lines. Hence, if at least one $m_{i} < 1$ ,

$$ \begin{align*} \bigg(\dfrac{S_{D}^{\Omega}(z)}{s}\bigg)^{1/\alpha} \leq H_{D}^{\Omega^{c}}(z) \leq H_{D}^{\Omega^{k}}(z),\quad z\in D.\\[-38pt] \end{align*} $$

Remark 2.2. In the case $\Omega = \mathbb {B}^{n}$ , we can take $\alpha = \beta = 1$ . It follows that Theorem 2.1 implies (1.2).

Theorem 2.3. Let $\Omega $ be as in (1.1). If K is a compact subset of $\Omega $ such that $D = \Omega \setminus K$ is connected, then:

1. (1) $S_{D}^{\Omega }(z) \geq (d_{c_{\Omega }}^{K}(z))^{\beta }$ if $\Omega $ is homogeneous;

2. (2) $S_{D}^{\Omega }(z) \leq (d_{c_{\Omega }}^{\partial K}(z))^{\alpha }$ if all $m_{i} \geq 1$ ;

3. (3) $S_{D}^{\Omega }(z) \leq s(d_{c_{\Omega }}^{\partial K}(z))^{\alpha }$ if at least one $m_{i} < 1$ .

For the proof of Theorem 2.3, we need the following results.

Result 2.4 [10, Theorem 1.2.6].

Let $\Omega \subseteq \mathbb {C}^{n}$ be a domain. If $K \subset \Omega $ is a compact set such that $D = \Omega \setminus K$ is connected, then each holomorphic function f on D extends to a holomorphic function F on $\Omega $ .

Result 2.5 [9, Proposition 2.2.15].

Let $\Omega \subseteq \mathbb {C}^{n}$ be a balanced domain. Then, $\Omega $ is pseudoconvex if and only if the Minkowski function $\rho _{\Omega }$ is plurisubharmonic.

Proof of Theorem 2.3.

For part (1), let $g : \Omega \to \Omega $ be an automorphism of $\Omega $ such that $g(z) = 0$ for some $z\in D$ . Then, $h = g\vert _D : D\to \Omega $ is an injective holomorphic mapping with $h(z) = 0$ . We claim that $\Omega ((d_{c_{\Omega }}^{K}(z))^{\beta }) \subseteq h(D) \subseteq \Omega $ . To prove this, let $w = (w_{1}, w_{2},\ldots , w_{s})\in \Omega ((d_{c_{\Omega }}^{K}(z))^{\beta })$ . By (2.2),

(2.6) $$ \begin{align} (d_{c_{\Omega}}^{K}(z))^{\beta}> \sum\limits_{i\in I_{k}}||w_{i}||^{m_{i}} \geq (\tanh c_{\Omega}(0, w))^{\beta} \end{align} $$

for $1 \leq k \leq p$ . Since g is an automorphism, it follows that

(2.7) $$ \begin{align} (\tanh c_{\Omega}(0, w))^{\beta} = (\tanh c_{g(\Omega)}(g(z), g(w')))^{\beta} = (\tanh c_{\Omega}(z, w'))^{\beta} \end{align} $$

for some $w'\in \Omega $ with $w = g(w')$ . By (2.6) and (2.7), $\tanh c_{\Omega }(z, w') < d_{c_{\Omega }}^{K}(z) = \min _{w\in K} \tanh [c_{\Omega }(z, w)]$ . This implies that $w'\notin K$ , which verifies our claim. Hence,

$$ \begin{align*}S_{D}^{\Omega}(z) \geq (d_{c_{\Omega}}^{K}(z))^{\beta}.\end{align*} $$

For part (2), assume that $S_{D}^{\Omega }(z) = r> 0$ for some $z\in D$ . By [1, Theorem 2.5], there exists an injective holomorphic mapping $f : D \to \Omega $ such that $f(z) = 0$ and $\Omega (r) \subseteq f(D) \subseteq \Omega $ . By Result 2.4, there is a holomorphic mapping $F : \Omega \to \mathbb {C}^{n}$ such that ${F = f\vert _\Omega} $ . By Result 2.5 and following the argument used in [15, Theorem 2.1], $F(\Omega )\subseteq \Omega $ . It is easy to see that $F(\partial K)\cap F(D) = \emptyset $ .

Next, we show that $r^{1/\alpha } \leq d_{c_{\Omega }}^{\partial K}(z)$ . If possible, let $r^{1/\alpha }> d_{c_{\Omega }}^{\partial K}(z)$ . Assume that $d_{c_{\Omega }}^{\partial K}(z) = \tanh c_{\Omega }(z, a)$ for some $a = (a_{1}, a_{2},\ldots , a_{s}) \in \partial K$ and $F(a)= (w_{1}', w_{2}',\ldots , w_{s}')$ . Therefore, by (2.2),

$$ \begin{align*}r^{1/\alpha}> \tanh c_{\Omega}(z, a) \geq \tanh c_{\Omega}(0, F(a))\geq \bigg(\sum\limits_{i\in I_{k}}||w_{i}'||^{m_{i}}\bigg)^{1/\alpha}\end{align*} $$

for $1 \leq k \leq p$ . Thus, $F(a) \in \Omega (r)$ . This is a contradiction because $F(\partial K)\cap F(D) = \emptyset $ . Hence, $S_{D}^{\Omega }(z) \leq (d_{c_{\Omega }}^{\partial K}(z))^{\alpha }$ .

For part (3), first assume that there is $m_{i}\geq 1$ for some i. By following similar arguments to those in part (2), we show that $({r}/{s})^{1/\alpha } \leq d_{c_{\Omega }}^{\partial K}(z)$ . If possible, let $({r}/{s})^{1/\alpha }> d_{c_{\Omega }}^{\partial K}(z)$ . Let $d_{c_{\Omega }}^{\partial K}(z) = \tanh c_{\Omega }(z, a)$ for some $a = (a_{1}, a_{2},\ldots , a_{s}) \in \partial K$ and $F(a)= (w_{1}', w_{2}',\ldots , w_{s}')$ , then

$$ \begin{align*}\bigg(\dfrac{r}{s}\bigg)^{1/\alpha}> \tanh c_{\Omega^{\beta}}(0, F(a))= \bigg(\sum\limits_{i\in I_{k}}||w_{i}'||^{\beta}\bigg)^{1/\beta}\end{align*} $$

for $1 \leq k \leq p$ so that $F(a) \in \Omega ^{\beta }(({r}/{s})^{\beta /\alpha })$ . It is easy to see that $\Omega ^{\beta }(({r}/{s})^{\beta /\alpha })\subseteq \Omega (r)$ . Thus, we get $F(a) \in \Omega (r)$ . This is a contradiction because $F(\partial K)\cap F(D) = \emptyset $ . Hence, $S_{D}^{\Omega }(z) \leq s(d_{c_{\Omega }}^{\partial K}(z))^{\alpha }$ . If all $m_{i} < 1$ , take $\beta = 1$ in these arguments and the proof follows the same lines.

Corollary 2.6. Let $\Omega $ in (1.1) be homogeneous such that $m_i = m \geq 1$ for all i. If K is a compact subset of $\Omega $ and $D = \Omega \setminus \partial K$ is connected, then

$$ \begin{align*}S_{D}^{\Omega}(z) = (d_{c_{\Omega}}^{\partial K}(z))^{m},\quad z\in D.\end{align*} $$

Corollary 2.7. Let $\Omega $ in (1.1) be homogeneous and $D = \Omega \setminus K$ as in Theorem 2.3. Then:

1. (1) $H_{D}^{\Omega ^{k}}(z) \geq H_{D}^{\Omega ^{c}}(z) \geq (d_{c_{\Omega }}^{K}(z))^{\beta ^{2}/\alpha ^{2}}$ for $z\in D$ if all $m_{i} \geq 1$ ;

2. (2) $H_{D}^{\Omega ^{k}}(z) \geq H_{D}^{\Omega ^{c}}(z) \geq \dfrac {(d_{c_{\Omega }}^{K}(z))^{\beta /\alpha }}{s^{1/\alpha }}$ for $z\in D$ if at least one $m_{i} < 1$ .

Theorem 2.8. Let $\Omega $ in (1.1) be homogeneous and K be a proper analytic subset of $\Omega $ . Then, for $D = \Omega \setminus \partial K$ :

1. (1) $(d_{c_{\Omega }}^{\partial K}(z))^{\beta ^{2}/\alpha ^{2}} \leq H_{D}^{\Omega ^{c}}(z) \leq (d_{c_{\Omega }}^{\partial K}(z))^{\alpha ^{2}/\beta ^{2}}$ for $z\in D$ if all $m_{i} \geq 1$ ;

2. (2) $\dfrac {(d_{c_{\Omega }}^{\partial K}(z))^{\beta /\alpha }}{s^{1/\alpha }} \leq H_{D}^{\Omega ^{c}}(z) \leq (d_{c_{\Omega }}^{\partial K}(z))^{\alpha ^{2}/\beta ^{2}}$ for $z\in D$ if at least one $m_{i} < 1$ .

Proof. For part (1), by Theorems 2.1(1) and 2.3(1),

$$ \begin{align*} H_{D}^{\Omega^{c}}(z) \geq (d_{c_{\Omega}}^{\partial K}(z))^{\beta^{2}/\alpha^{2}},\quad z\in D. \end{align*} $$

We show that $H_{D}^{\Omega ^{c}}(z) \leq (d_{c_{\Omega }}^{\partial K}(z))^{\alpha ^{2}/\beta ^{2}}$ . Suppose in contrast that $H_{D}^{\Omega ^{c}}(z)> (d_{c_{\Omega }}^{\partial K}(z))^{\alpha ^{2}/\beta ^{2}}$ . Then, there exists r such that $\tanh r> (d_{c_{\Omega }}^{\partial K}(z))^{\alpha ^{2}/\beta ^{2}} \geq d_{c_{\Omega }}^{\partial K}(z)$ , and an injective holomorphic mapping $f : \Omega \to D$ such that $f(0) = z$ and ${B_{D}^{c}(z, r) \subseteq f(\Omega ) \subseteq D}$ . Let $d_{c_{\Omega }}^{\partial K}(z) = \tanh c_{\Omega }(z, a)$ for some $a\in \partial K$ . By the Riemann removable singularity theorem, $c_{D}(z_{1}, z_{2}) = c_{\Omega }(z_{1}, z_{2})$ for all $z_{1}, z_{2} \in D$ . This implies that ${B_{D}^{c}(z, r) = \lbrace \xi \in D : c_{\Omega }(z, \xi ) < r \rbrace} $ . It is easy to see that $a \in B_{\Omega }^{c}(z, r)$ . Since the topology induced by the Carathéodory pseudometric on a bounded domain is equivalent to the Euclidean topology, it follows that there exists $\epsilon> 0$ such that $\mathbb {B}^{n}(a, \epsilon ) \subseteq B_{\Omega }^{c}(z, r)$ . Then, $\mathbb {B}^{n}(a, \epsilon )\setminus \partial K \subseteq B_{D}^{c}(z, r) \subseteq f(\Omega )$ .

Let $g = f^{-1} : \mathbb {B}^{n}(a, \epsilon )\setminus \partial K \to \Omega $ . By the Riemann removable singularity theorem, there is a holomorphic mapping $h: \mathbb {B}^{n}(a, \epsilon )\to \overline {\Omega }$ such that $h(\xi ) = g(\xi )$ for all ${\xi \in \mathbb {B}^{n}(a, \epsilon )\setminus \partial K}$ . By Result 2.5 and following the argument used in [15, Theorem 2.8], $\rho _{\Omega }(h(\xi )) = 1$ for all $\xi \in \mathbb {B}^{n}(a, \epsilon )\cap \partial K$ . By the maximum principal of plurisubharmonic functions, $\rho _{\Omega }(h(\xi )) \equiv 1$ , which is a contradiction.

For part (2), by Theorems 2.1(2) and 2.3(1),

$$ \begin{align*} H_{D}^{\Omega^{c}}(z) \geq \dfrac{(d_{c_{\Omega}}^{\partial K}(z))^{\beta/\alpha}}{s^{1/\alpha}},\quad z\in D. \end{align*} $$

Similarly, as argued in part (1),

$$ \begin{align*} H_{D}^{\Omega^{c}}(z) \leq (d_{c_{\Omega}}^{\partial K}(z))^{\alpha^{2}/\beta^{2}},\quad z\in D.\\[-42pt]\end{align*} $$

Corollary 2.9. Let $\Omega $ in (1.1) be homogeneous with $m_i = m \geq 1$ for all i and let K be a proper analytic subset of $\Omega $ . Then, for $D = \Omega \setminus \partial K$ ,

$$ \begin{align*}H_{D}^{\Omega^{c}}(z) = d_{c_{\Omega}}^{\partial K}(z),\quad z\in D.\end{align*} $$

3 Nonplurisubharmonic ${S_{D}^{\Omega }}$

Theorem 3.1. Let $\Omega \subseteq \mathbb {C}^{2}$ be a domain of the form (1.1) such that ${m_i = m}$ for all i. Assume that $v = \max \lbrace \sum _{i\in I_{k}} r_{i}^{m/2}, 1 \leq k \leq p\rbrace $ . Choose $\epsilon $ such that ${0\kern1.3pt{<}\kern1.3pt\epsilon \kern1.3pt{<}\kern1.3pt r\kern1.3pt{<}\kern1.3pt (1/v)^{1/m}\kern1.3pt{<}\kern1.3pt 1}$ , $\overline {\mathbb {D}^{2}(0, r)}\subset \Omega $ and $\mathbb {B}^{2}(Q, \epsilon )\subset \Omega $ for $Q = (0, r)$ . Let ${K = \partial \mathbb {D}^{2}(0, r)\setminus \mathbb {B}^{2}(Q, \epsilon )}$ and ${D = \Omega \setminus K}$ . Then, $S_{D}^{\Omega }$ is not plurisubharmonic.

Proof. Denote $H = \lbrace z = (z_{1}, z_{2})\in \mathbb {C}^{n} : z_{2} = 0\rbrace $ . We show that $S_{D}^{\Omega }(0) \geq r^{m}$ . To see this, consider the identity function $I : D \to \Omega $ . Clearly, I is an injective holomorphic mapping with $I(0) = 0$ . It is easy to see that $\Omega (r^{m})\subseteq I(D)$ . Thus,

$$ \begin{align*} S_{D}^{\Omega}(0) \geq r^{m}. \end{align*} $$

Let us assume that $m \geq 1$ . Observe that $\mathbb {D}^{2}(0, r)\cap H = \lbrace z = (z_{1}, 0) : |z_{1}| < r\rbrace \subseteq D\cap H$ . For $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ with $0 < |z_{1}| < r$ , by Theorem 2.3(2),

(3.1) $$ \begin{align} S_{D}^{\Omega}(z) \leq \Big(\min_{w\in \partial K}\tanh [c_{\Omega}(z, w)]\Big)^{m}. \end{align} $$

Let $w' = (az_{1}, 0)$ , where $a = {r}/{|z_{1}|}$ . Then, $w'\in \partial K$ and therefore, by (3.1),

(3.2) $$ \begin{align} S_{D}^{\Omega}(z) \leq \Big(\min_{w\in \partial K}\tanh [c_{\Omega}(z, w)]\Big)^{m} \leq (\tanh [c_{\Omega}(z, w')])^{m}. \end{align} $$

It is easy to see that $\mathbb {D}^{2}(0, ({1}/{v})^{1/m})\subseteq \Omega $ . By the decreasing property of the Carathéodory metric,

(3.3) $$ \begin{align} (\tanh c_{\Omega}(z, w'))^{m}\leq \bigg(\tanh c_{\mathbb{D}^{2}}\bigg(\dfrac{z}{(1/v)^{1/m}}, \dfrac{w'}{(1/v)^{1/m}}\bigg)\bigg)^{m}. \end{align} $$

By (3.2), (3.3) and (2.1),

(3.4) $$ \begin{align} S_{D}^{\Omega}(z) \leq \bigg| \dfrac{v^{1/m}z_{1}(a- 1)}{1- v^{2/m}a\overline{z}_{1} z_{1}} \bigg|^m \leq \bigg(\dfrac{v^{1/m}(r - |z_{1}|)}{1- v^{2/m}r|z_{1}|}\bigg)^{m}. \end{align} $$

Note that

(3.5) $$ \begin{align} \bigg(\dfrac{v^{1/m}(r - |z_{1}|)}{1- v^{2/m}r|z_{1}|}\bigg)^{m} < r^{m} \end{align} $$

for $|z_{1}|> \eta = {r(v^{1/m}-1)}/{v^{1/m}(1-r^{2}v^{1/m})}$ . By (3.4) and (3.5),

(3.6) $$ \begin{align} S_{D}^{\Omega}(z) \leq S_{D}^{\Omega}(0) \end{align} $$

for $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ with $|z_{1}|> \eta $ . Observe that $\eta < r$ because $r < ({1}/{v})^{1/m}$ . Let the maximum of $S_{D}^{\Omega }(z)$ for $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ and $|z_{1}| \leq \eta $ be attained at some $\xi \in \overline {\mathbb {D}(0, \eta )}$ . Then,

(3.7) $$ \begin{align} S_{D}^{\Omega}(z) \leq S_{D}^{\Omega}(\xi) \end{align} $$

for $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ with $|z_{1}| \leq \eta $ . By (3.6) and (3.7),

$$ \begin{align*}S_{D}^{\Omega}(z) \leq \max(S_{D}^{\Omega}(0), S_{D}^{\Omega}(\xi))\end{align*} $$

for all $z\in \mathbb {D}^{2}(0, r)\cap H$ . This implies that $S_{D}^{\Omega }\vert _{\mathbb {D}^{2}(0, r)\cap H}$ does not satisfy the maximum principle. Hence, $S_{D}^{\Omega }$ is not plurisubharmonic.

Let us now assume that $m < 1$ . Similarly, as argued above, by Theorem 2.3(3),

$$ \begin{align*} S_{D}^{\Omega}(z) \leq s\bigg| \dfrac{v^{1/m}z_{1}(a- 1)}{1- v^{2/m}a\overline{z}_{1} z_{1}} \bigg|^m \leq s\bigg(\dfrac{v^{1/m}(r - |z_{1}|)}{1- v^{2/m}r|z_{1}|}\bigg)^{m}. \end{align*} $$

Note that

$$ \begin{align*} s\bigg(\dfrac{v^{1/m}(r - |z_{1}|)}{1- v^{2/m}r|z_{1}|}\bigg)^{m} < r^{m} \end{align*} $$

for $|z_{1}|> \eta ' = {r(v^{1/m}s^{1/m}-1)}/{v^{1/m}(s^{1/m}-r^{2}v^{1/m})}$ . This implies that

(3.8) $$ \begin{align} S_{D}^{\Omega}(z) \leq S_{D}^{\Omega}(0) \end{align} $$

for $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ with $|z_{1}|> \eta '$ . Observe that $\eta ' < r$ because $r < ({1}/{v})^{1/m}$ . Let the maximum of $S_{D}^{\Omega }(z)$ for $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ and $|z_{1}| \leq \eta '$ be attained at some $\xi ' \in \overline {\mathbb {D}(0, \eta ')}$ . Then,

(3.9) $$ \begin{align} S_{D}^{\Omega}(z) \leq S_{D}^{\Omega}(\xi') \end{align} $$

for $z = (z_{1}, 0)\in \mathbb {D}^{2}(0, r)\cap H$ with $|z_{1}| \leq \eta '$ . By (3.8) and (3.9),

$$ \begin{align*}S_{D}^{\Omega}(z) \leq \max(S_{D}^{\Omega}(0), S_{D}^{\Omega}(\xi'))\end{align*} $$

for all $z\in \mathbb {D}^{2}(0, r)\cap H$ . This implies that $S_{D}^{\Omega }\vert _{\mathbb {D}^{2}(0, r)\cap H}$ does not satisfy the maximum principle. Hence, $S_{D}^{\Omega }$ is not plurisubharmonic.

The next result is a generalisation of Theorem 3.1 for higher dimensions.

Theorem 3.2. Let $\Omega \subseteq \mathbb {C}^{n}$ be a domain of the form (1.1) such that $m_i = m$ for all i. In addition, assume that $v = \max \lbrace \sum _{i\in I_{k}} r_{i}^{m/2}, 1 \leq k \leq p\rbrace $ . Choose $\epsilon $ such that $0<\epsilon <r< (1/v)^{1/m}<1$ , $\overline {\mathbb {D}^{n}(0, r)}\subset \Omega $ and $\mathbb {B}^{n}(Q, \epsilon )\subset \Omega $ for $Q = (0, 0,\ldots , r)$ . Let $K = \partial \mathbb {D}^{n}(0, r)\setminus \mathbb {B}^{n}(Q, \epsilon )$ and $D = \Omega \setminus K$ . Then, $S_{D}^{\Omega }$ is not plurisubharmonic.

Proof. The proof is similar to that for Theorem 3.1 and we omit the details.