Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 11
Boundedness Criteria for Generalized Hankel Conjugate Transformations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 147-153
-
- Article
-
- You have access
- Export citation
- Cited by 11
Upper Bounds on |L(1, χ)| and Applications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 794-815
-
- Article
-
- You have access
- Export citation
- Cited by 11
Associated Continuous Hahn Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1263-1280
-
- Article
-
- You have access
- Export citation
- Cited by 11
The Bishop-Phelps-Bollobàs Property for Compact Operators
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 53-57
-
- Article
-
- You have access
- Export citation
- Cited by 11
A Mixed Problem for Normal Hyperbolic Linear Partial Differential Equations of Second Order
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-160
-
- Article
-
- You have access
- Export citation
- Cited by 11
C*-Convexity and Matricial Ranges
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 280-297
-
- Article
-
- You have access
- Export citation
- Cited by 11
Approximations to the Area of ann-Dimensional Ellipsoid
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-282
-
- Article
-
- You have access
- Export citation
- Cited by 11
Central Idempotent Measures on Unitary Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 719-725
-
- Article
-
- You have access
- Export citation
- Cited by 11
Tubes, Cohomology with Growth Conditions and an Application to the Theta Correspondence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-37
-
- Article
-
- You have access
- Export citation
- Cited by 11
An Automorphic Theta Module for Quaternionic Exceptional Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 737-756
-
- Article
-
- You have access
- Export citation
- Cited by 11
A Note on Some Perfect Squared Squares
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 304-308
-
- Article
-
- You have access
- Export citation
- Cited by 11
Combinatorial Matrices with Small Determinants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 756-762
-
- Article
-
- You have access
- Export citation
- Cited by 11
The Number of Generators of a Linear p-Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 851-858
-
- Article
-
- You have access
- Export citation
- Cited by 11
The Primitive Spectrum and Category
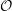 ${\mathcal{O}}$ for the Periplectic Lie Superalgebra
${\mathcal{O}}$ for the Periplectic Lie Superalgebra
- Part of:
-
- Published online by Cambridge University Press:
- 16 November 2018, pp. 625-655
-
- Article
-
- You have access
- Export citation
- Cited by 11
On Steenrod's Problem for Cyclic p-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 421-428
-
- Article
-
- You have access
- Export citation
- Cited by 11
On Representations as a Sum of Consecutive Integers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 399-405
-
- Article
-
- You have access
- Export citation
- Cited by 11
Mixing on Sequences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 339-352
-
- Article
-
- You have access
- Export citation
- Cited by 11
Two Results Concerning the Zeros of Functions with Finite Dirichlet Integral
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 312-316
-
- Article
-
- You have access
- Export citation
- Cited by 11
Infinitely Periodic Knots
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 17-28
-
- Article
-
- You have access
- Export citation
- Cited by 11
Sur La Classification Des Symetries Des C*-Algebres UHF
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 496-523
-
- Article
-
- You have access
- Export citation
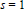

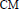
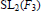
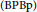
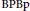
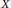

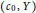
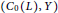

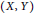
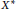
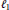
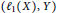
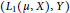

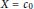
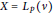

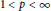
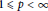
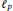
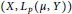
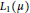
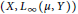


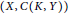
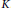
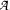 , then for every
, then for every 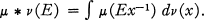
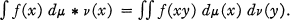
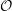
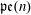
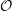
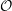

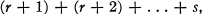
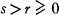 . It is shown that
. It is shown that 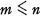 for which
for which 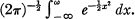
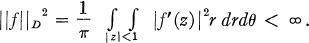
 . The condition above can be restated in terms of Taylor coefficients; if
. The condition above can be restated in terms of Taylor coefficients; if 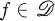 if and only if
if and only if 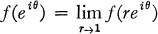
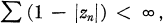
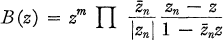
 une symétrie de
une symétrie de  ; on associe à θ un entier généralisé
; on associe à θ un entier généralisé 