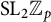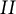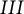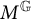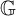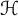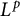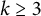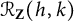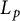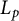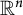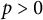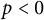FirstView articles
Contents
Article
Inequalities of the ℓp-operator norm for block matrices
- Part of:
-
- Published online by Cambridge University Press:
- 26 January 2026, pp. 1-12
-
- Article
- Export citation
Liminal
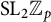 $\mathrm {SL}_2 \mathbb{Z}_{p}$-representations and odd-th cyclic covers of genus one two-bridge knots
$\mathrm {SL}_2 \mathbb{Z}_{p}$-representations and odd-th cyclic covers of genus one two-bridge knots
- Part of:
-
- Published online by Cambridge University Press:
- 23 January 2026, pp. 1-11
-
- Article
- Export citation
Fixed-point permanence under actions by finite quantum groups
- Part of:
-
- Published online by Cambridge University Press:
- 16 January 2026, pp. 1-9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct sums of Chow motives and Rost nilpotence
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2026, pp. 1-14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Dirichlet spaces with zero sets containing all Blaschke sequences
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2026, pp. 1-8
-
- Article
- Export citation
Signature characters of invariant Hermitian forms on irreducible Verma modules of singular infinitesimal character and Hall–Littlewood polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 09 January 2026, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The weak-type (1,1) estimate of the
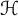 $\mathcal {H}$-harmonic Bergman projection
$\mathcal {H}$-harmonic Bergman projection
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2026, pp. 1-9
-
- Article
- Export citation
Restriction problem for mod p representations of GL2 over a finite field
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2026, pp. 1-14
-
- Article
- Export citation
The existence of Hopf bifurcation for a delayed Holling–Tanner type predator–prey model
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-13
-
- Article
- Export citation
On the power growth order of homeomorphisms of certain classes
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-22
-
- Article
- Export citation
Overpartitions with parts separated by parity
- Part of:
-
- Published online by Cambridge University Press:
- 05 January 2026, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grassmannian forms of LXYZ's
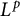 $L^p$ affine Sobolev inequality chain
$L^p$ affine Sobolev inequality chain
- Part of:
-
- Published online by Cambridge University Press:
- 02 January 2026, pp. 1-17
-
- Article
- Export citation
Čech cohomology of infinite projective spaces, flag manifolds, and related spaces
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quelques résultats sur les anneaux de Lie qui n’ont pas de chaîne infinie de centralisateurs
- Part of:
-
- Published online by Cambridge University Press:
- 23 December 2025, pp. 1-13
-
- Article
- Export citation
The boundary rigidity for holomorphic self-maps on bounded symmetric domains with an interior fixed point
- Part of:
-
- Published online by Cambridge University Press:
- 17 December 2025, pp. 1-4
-
- Article
- Export citation
Explicit sumset sizes in additive number theory
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2025, pp. 1-12
-
- Article
- Export citation
The
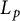 $L_p$ Gauss image problem for C-pseudo-cones
$L_p$ Gauss image problem for C-pseudo-cones
- Part of:
-
- Published online by Cambridge University Press:
- 02 December 2025, pp. 1-12
-
- Article
- Export citation
Polygons of unit area with vertices in sets of infinite planar measure
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-16
-
- Article
- Export citation
Sharp bounds for higher Steklov–Dirichlet eigenvalues on domains with spherical holes
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-20
-
- Article
- Export citation
Multiplicity one theorem for general Spin groups: The Archimedean case
- Part of:
-
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-17
-
- Article
- Export citation