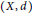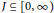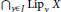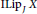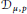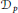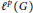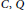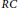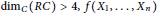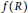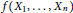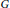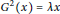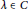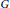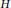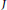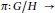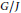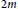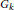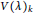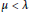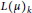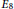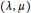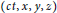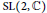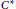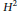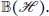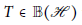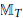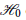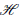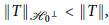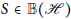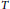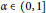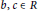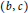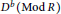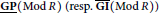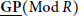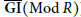Contents
Research Article
Character Amenability of the Intersection of Lipschitz Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-689
-
- Article
-
- You have access
- Export citation
Qp Spaces and Dirichlet Type Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 690-704
-
- Article
-
- You have access
- Export citation
Envelope Approach to Degenerate Complex Monge–Ampére Equations on Compact Kähler Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 705-711
-
- Article
-
- You have access
- Export citation
Disjoint Hypercyclicity and Weighted Translations on Discrete Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 712-720
-
- Article
-
- You have access
- Export citation
On Identities with Composition of Generalized Derivations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 721-735
-
- Article
-
- You have access
- Export citation
Levi's Problem for Pseudoconvex Homogeneous Manifolds
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 736-746
-
- Article
-
- You have access
- Open access
- Export citation
Injectivity of Generalized Wronski Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 747-761
-
- Article
-
- You have access
- Export citation
Maximal Weight Composition Factors for Weyl Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 762-773
-
- Article
-
- You have access
- Export citation
On the Structure of the Schild Group in Relativity Theory
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 774-790
-
- Article
-
- You have access
- Export citation
Reduction to Dimension Two of the Local Spectrum for an AH Algebra with the Ideal Property
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 791-806
-
- Article
-
- You have access
- Export citation
The Shifted Classical Circulant and Skew Circulant Splitting Iterative Methods for Toeplitz Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 807-815
-
- Article
-
- You have access
- Export citation
Characterizations of Operator Birkhoff–James Orthogonality
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 816-829
-
- Article
-
- You have access
- Export citation
Generalized Torsion Elements and Bi-orderability of 3-manifold Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 830-844
-
- Article
-
- You have access
- Export citation
Continuity of Convolution and SIN Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-854
-
- Article
-
- You have access
- Export citation
The Kottman Constant for α-HÖlder Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 855-860
-
- Article
-
- You have access
- Export citation
Characterizations of Outer Generalized Inverses
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 861-871
-
- Article
-
- You have access
- Export citation
Rational Function Operators from Poisson Integrals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 872-878
-
- Article
-
- You have access
- Export citation
Triangulated Equivalences Involving Gorenstein Projective Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 879-890
-
- Article
-
- You have access
- Export citation