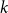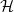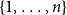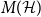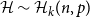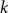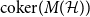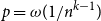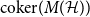1. Introduction
Let
![]() $\mathcal{H}$
be a
$\mathcal{H}$
be a
![]() $k$
-uniform hypergraph on vertex set
$k$
-uniform hypergraph on vertex set
![]() $[n]$
. We associate to
$[n]$
. We associate to
![]() $\mathcal{H}$
a matrix
$\mathcal{H}$
a matrix
![]() $M \;:\!=\; M(\mathcal{H})$
with rows indexed by the vertices and columns indexed by the edges of
$M \;:\!=\; M(\mathcal{H})$
with rows indexed by the vertices and columns indexed by the edges of
![]() $\mathcal{H}$
. For
$\mathcal{H}$
. For
![]() $e = \{v_1, v_2, \ldots, v_k\}$
each
$e = \{v_1, v_2, \ldots, v_k\}$
each
![]() $v_i \in [n]$
with
$v_i \in [n]$
with
![]() $v_1 \lt v_2 \lt \cdots \lt v_k$
,
$v_1 \lt v_2 \lt \cdots \lt v_k$
,
![]() $M(v_i, e) \;:\!=\; (\!-\!1)^{i + 1}$
for
$M(v_i, e) \;:\!=\; (\!-\!1)^{i + 1}$
for
![]() $1 \leq i \leq k$
and
$1 \leq i \leq k$
and
![]() $M(v, e) \;:\!=\; 0$
for
$M(v, e) \;:\!=\; 0$
for
![]() $v \notin e$
. Our primary object of study is the cokernel of
$v \notin e$
. Our primary object of study is the cokernel of
![]() $M(\mathcal{H})$
when
$M(\mathcal{H})$
when
![]() $\mathcal{H}$
is a random hypergraph.
$\mathcal{H}$
is a random hypergraph.
The motivation for this model comes from a question about random simplicial complexes. Recall that the Linial–Meshulam model, introduced in [Reference Linial and Meshulam10, Reference Meshulam and Wallach13], denoted
![]() $Y_d(n, p)$
is the probability space on
$Y_d(n, p)$
is the probability space on
![]() $d$
-dimensional simplicial complexes on
$d$
-dimensional simplicial complexes on
![]() $n$
vertices with complete
$n$
vertices with complete
![]() $(d - 1)$
-skeleton sampled by including each
$(d - 1)$
-skeleton sampled by including each
![]() $d$
-face independently with probability
$d$
-face independently with probability
![]() $p$
. Observe that
$p$
. Observe that
![]() $Y_1(n, p)$
is the Erdős–Rényi random graph model. Since the Linial–Meshulam model was first introduced much of the research has been to establish thresholds for topological properties that generalise thresholds for graph properties. One of the most important thresholds in
$Y_1(n, p)$
is the Erdős–Rényi random graph model. Since the Linial–Meshulam model was first introduced much of the research has been to establish thresholds for topological properties that generalise thresholds for graph properties. One of the most important thresholds in
![]() $Y_d(n, p)$
is the one-sided sharp threshold for nonvanishing of the
$Y_d(n, p)$
is the one-sided sharp threshold for nonvanishing of the
![]() $d$
th homology group due to Aronshtam, Linial, and Peled [Reference Aronshtam and Linial2, Reference Linial and Peled11]. Namely for each
$d$
th homology group due to Aronshtam, Linial, and Peled [Reference Aronshtam and Linial2, Reference Linial and Peled11]. Namely for each
![]() $d \geq 2$
, there is an explicit constant
$d \geq 2$
, there is an explicit constant
![]() $c_d$
defined in [Reference Aronshtam and Linial2] so that if
$c_d$
defined in [Reference Aronshtam and Linial2] so that if
![]() $p = c/n$
with
$p = c/n$
with
![]() $c \lt c_d$
then the
$c \lt c_d$
then the
![]() $d$
th homology group of
$d$
th homology group of
![]() $Y \sim Y_d(n, p)$
with rational coefficients is generated by Poisson-distributed embedded copies of the
$Y \sim Y_d(n, p)$
with rational coefficients is generated by Poisson-distributed embedded copies of the
![]() $(d + 1)$
-simplex boundary in
$(d + 1)$
-simplex boundary in
![]() $Y_d(n, p)$
[Reference Linial and Peled11]. On the other hand for
$Y_d(n, p)$
[Reference Linial and Peled11]. On the other hand for
![]() $c \gt c_d$
, [Reference Aronshtam and Linial2] shows that with high probability
$c \gt c_d$
, [Reference Aronshtam and Linial2] shows that with high probability
![]() $Y \sim Y_d(n, p)$
has
$Y \sim Y_d(n, p)$
has
![]() $d$
th Betti number of order
$d$
th Betti number of order
![]() $\Theta (n^d)$
with high probability.
$\Theta (n^d)$
with high probability.
While we don’t yet have a good understanding of what happens inside the critical window for
![]() $p$
near
$p$
near
![]() $c_d/n$
, experiments conducted by Kahle, Lutz, Newman, and Parsons [Reference Kahle, Lutz, Newman and Parsons9] demonstrate strongly that the homology within the critical window is very interesting. More specifically, the experiments conducted in [Reference Kahle, Lutz, Newman and Parsons9] witness a torsion burst in the
$c_d/n$
, experiments conducted by Kahle, Lutz, Newman, and Parsons [Reference Kahle, Lutz, Newman and Parsons9] demonstrate strongly that the homology within the critical window is very interesting. More specifically, the experiments conducted in [Reference Kahle, Lutz, Newman and Parsons9] witness a torsion burst in the
![]() $(d - 1)$
st homology group within the critical window. An instance of the experiment in [Reference Kahle, Lutz, Newman and Parsons9] starts with the complete graph on
$(d - 1)$
st homology group within the critical window. An instance of the experiment in [Reference Kahle, Lutz, Newman and Parsons9] starts with the complete graph on
![]() $n$
vertices, and a 2-complex is constructed from this graph by adding triangles one at a time in random order. That is, at each step one picks uniformly at random a triangle on the ground set that is not already included in the complex and adds it. In this way we turn
$n$
vertices, and a 2-complex is constructed from this graph by adding triangles one at a time in random order. That is, at each step one picks uniformly at random a triangle on the ground set that is not already included in the complex and adds it. In this way we turn
![]() $Y_2(n, p)$
into a stochastic process and can study how the two interesting homology groups evolve. Early on, most of the time a new triangle is added, the free rank of
$Y_2(n, p)$
into a stochastic process and can study how the two interesting homology groups evolve. Early on, most of the time a new triangle is added, the free rank of
![]() $H_1$
drops by one, but occasionally a tetrahedron boundary is completed and so the rank of
$H_1$
drops by one, but occasionally a tetrahedron boundary is completed and so the rank of
![]() $H_2$
increases by one instead. Moreover, at the early stages
$H_2$
increases by one instead. Moreover, at the early stages
![]() $H_1$
is torsion-free. However, right around the critical density for the phase transition in
$H_1$
is torsion-free. However, right around the critical density for the phase transition in
![]() $H_2$
established in [Reference Aronshtam and Linial2, Reference Linial and Peled11], one observes large torsion in the first homology group. In a particular instance shown as Table 1 in [Reference Kahle, Lutz, Newman and Parsons9] with
$H_2$
established in [Reference Aronshtam and Linial2, Reference Linial and Peled11], one observes large torsion in the first homology group. In a particular instance shown as Table 1 in [Reference Kahle, Lutz, Newman and Parsons9] with
![]() $n = 75$
, when the 2470th triangle is added, torsion appears in the first homology group. At that point in this experiment the first homology group was
$n = 75$
, when the 2470th triangle is added, torsion appears in the first homology group. At that point in this experiment the first homology group was
![]() $\mathbb{Z}^{235} \times \mathbb{Z}/2\mathbb{Z}$
. What is even more interesting is that when the 2475th triangle is added in this particular run the torsion part of the first homology group has order larger than
$\mathbb{Z}^{235} \times \mathbb{Z}/2\mathbb{Z}$
. What is even more interesting is that when the 2475th triangle is added in this particular run the torsion part of the first homology group has order larger than
![]() $10^{26}$
, but when one more triangle is added this torsion drops to
$10^{26}$
, but when one more triangle is added this torsion drops to
![]() $\mathbb{Z}/2\mathbb{Z}$
. The details of which groups appear can be found in Table 1 of [Reference Kahle, Lutz, Newman and Parsons9]. Once this torsion is gone, we have apparently passed the homology threshold of [Reference Aronshtam and Linial2, Reference Linial and Peled11] and the rank of the second homology group starts to grow quickly.
$\mathbb{Z}/2\mathbb{Z}$
. The details of which groups appear can be found in Table 1 of [Reference Kahle, Lutz, Newman and Parsons9]. Once this torsion is gone, we have apparently passed the homology threshold of [Reference Aronshtam and Linial2, Reference Linial and Peled11] and the rank of the second homology group starts to grow quickly.
Table 1 Sample run of the random abelian group process with
![]() $n = 100$
and
$n = 100$
and
![]() $k = 3$
$k = 3$

Beyond gathering evidence about the existence of a torsion burst in the Linial–Meshulam model, [Reference Kahle, Lutz, Newman and Parsons9] also provides experimental evidence that the torsion groups that appear look like typical random abelian groups. More specifically, they appear to follow Cohen–Lenstra heuristics, a family of distributions on finite abelian groups first described in [Reference Cohen and Lenstra5]. This fits with the behaviour of torsion in other models of cokernels of random integer matrices such as sandpile groups of random graphs studied by [Reference Clancy, Kaplan, Leake, Payne and Wood4, Reference Mészáros14, Reference Wood19].
As the torsion in the
![]() $(d - 1)$
st homology group of a simplicial complex comes from the cokernel of the
$(d - 1)$
st homology group of a simplicial complex comes from the cokernel of the
![]() $d$
th boundary matrix, it seemed reasonable when conducting the experiments for [Reference Kahle, Lutz, Newman and Parsons9] to try and see if the same torsion burst behaviour occurred in a random matrix model. The
$d$
th boundary matrix, it seemed reasonable when conducting the experiments for [Reference Kahle, Lutz, Newman and Parsons9] to try and see if the same torsion burst behaviour occurred in a random matrix model. The
![]() $d$
th boundary matrix of a simplicial complex (when choosing orientations from an ordering on the vertices) is a matrix in which each column has exactly
$d$
th boundary matrix of a simplicial complex (when choosing orientations from an ordering on the vertices) is a matrix in which each column has exactly
![]() $(d + 1)$
nonzero entries and those nonzero entries alternate as
$(d + 1)$
nonzero entries and those nonzero entries alternate as
![]() $1, -1, 1, -1, \ldots, (\!-\!1)^{d + 1}$
. From this perspective when working on [Reference Kahle, Lutz, Newman and Parsons9] it made sense to run experiments to see what happens in a model of random matrices that have this structure but not the far more restrictive structure coming from the geometry of a simplicial complex, that is, the matrices described above as
$1, -1, 1, -1, \ldots, (\!-\!1)^{d + 1}$
. From this perspective when working on [Reference Kahle, Lutz, Newman and Parsons9] it made sense to run experiments to see what happens in a model of random matrices that have this structure but not the far more restrictive structure coming from the geometry of a simplicial complex, that is, the matrices described above as
![]() $M(\mathcal{H})$
for
$M(\mathcal{H})$
for
![]() $\mathcal{H}$
a
$\mathcal{H}$
a
![]() $(d + 1)$
-uniform hypergraph on
$(d + 1)$
-uniform hypergraph on
![]() $[n]$
. These experiments turned out to exhibit the same behaviour as
$[n]$
. These experiments turned out to exhibit the same behaviour as
![]() $Y_d(n, p)$
.
$Y_d(n, p)$
.
Random matrices with a fixed number of nonzero entries in each row have been considered in the past and [Reference Linial and Peled11] in particular mentions their similarity with
![]() $Y_d(n, p)$
. For example Pittel and Sorkin [Reference Pittel and Sorkin17] consider this same model for random matrices we describe here over
$Y_d(n, p)$
. For example Pittel and Sorkin [Reference Pittel and Sorkin17] consider this same model for random matrices we describe here over
![]() $\mathbb{Z}/2\mathbb{Z}$
in studying random instances of
$\mathbb{Z}/2\mathbb{Z}$
in studying random instances of
![]() $k$
-XORSAT and Cooper, Frieze, and Pegden [Reference Cooper, Frieze and Pegden6] prove that a random matrix over
$k$
-XORSAT and Cooper, Frieze, and Pegden [Reference Cooper, Frieze and Pegden6] prove that a random matrix over
![]() $\mathbb{Z}/2\mathbb{Z}$
with exactly
$\mathbb{Z}/2\mathbb{Z}$
with exactly
![]() $k$
1’s in each column exhibit a phase transition in the rank. The phase transitions described in [Reference Cooper, Frieze and Pegden6, Reference Pittel and Sorkin17] are perfectly analogous to the phase transition in homology of
$k$
1’s in each column exhibit a phase transition in the rank. The phase transitions described in [Reference Cooper, Frieze and Pegden6, Reference Pittel and Sorkin17] are perfectly analogous to the phase transition in homology of
![]() $Y_d(n, p)$
established by [Reference Aronshtam and Linial2, Reference Linial and Peled11] in quite a strong sense. In
$Y_d(n, p)$
established by [Reference Aronshtam and Linial2, Reference Linial and Peled11] in quite a strong sense. In
![]() $Y_d(n, c/n)$
with
$Y_d(n, c/n)$
with
![]() $c$
constant, if
$c$
constant, if
![]() $c$
is large enough that the average degree of a
$c$
is large enough that the average degree of a
![]() $(d - 1)$
-dimensional face exceeds
$(d - 1)$
-dimensional face exceeds
![]() $c_d$
then
$c_d$
then
![]() $Y \sim Y_d(n, c/n)$
asymptotically almost surely has nonvanishing
$Y \sim Y_d(n, c/n)$
asymptotically almost surely has nonvanishing
![]() $d$
th homology while for
$d$
th homology while for
![]() $c$
small enough that the average degree of
$c$
small enough that the average degree of
![]() $(d - 1)$
-dimensional face is smaller than
$(d - 1)$
-dimensional face is smaller than
![]() $c_d$
then
$c_d$
then
![]() $d$
-homology is generated by
$d$
-homology is generated by
![]() $(d + 1)$
-simplex boundaries. For this same
$(d + 1)$
-simplex boundaries. For this same
![]() $c_d$
, as is pointed out in [Reference Linial and Peled11], Pittel and Sorkin show that a random
$c_d$
, as is pointed out in [Reference Linial and Peled11], Pittel and Sorkin show that a random
![]() $n \times m$
matrix over
$n \times m$
matrix over
![]() $\mathbb{Z}/2\mathbb{Z}$
with exactly
$\mathbb{Z}/2\mathbb{Z}$
with exactly
![]() $d + 1$
1’s in each column will have nontrivial kernel when the average number of 1’s in each row exceeds
$d + 1$
1’s in each column will have nontrivial kernel when the average number of 1’s in each row exceeds
![]() $c_d$
and trivial kernel when this average is below
$c_d$
and trivial kernel when this average is below
![]() $c_d$
. Work of Cooper, Frieze, and Pegden [Reference Cooper, Frieze and Pegden6] refines this result to describe the asymptotic rank of the random
$c_d$
. Work of Cooper, Frieze, and Pegden [Reference Cooper, Frieze and Pegden6] refines this result to describe the asymptotic rank of the random
![]() $\mathbb{Z}/2\mathbb{Z}$
matrix on either side of the phase transition. It is at the phase transition of [Reference Pittel and Sorkin17] that experiments witness a torsion burst in our random matrix model.
$\mathbb{Z}/2\mathbb{Z}$
matrix on either side of the phase transition. It is at the phase transition of [Reference Pittel and Sorkin17] that experiments witness a torsion burst in our random matrix model.
As with the experiments for [Reference Kahle, Lutz, Newman and Parsons9] to see this torsion burst it seems necessary to view the cokernel of
![]() $M(\mathcal{H})$
for
$M(\mathcal{H})$
for
![]() $\mathcal{H}$
a random hypergraph as a stochastic process. That is we add columns one at a time and compute the cokernel at each step. The results of a sample run are shown in Table 1. The experiment was carried out using GAP [8].
$\mathcal{H}$
a random hypergraph as a stochastic process. That is we add columns one at a time and compute the cokernel at each step. The results of a sample run are shown in Table 1. The experiment was carried out using GAP [8].
Proving the existence of the torsion burst in
![]() $Y_d(n, p)$
seems to be quite a difficult problem without obvious tools to approach it. More tractable perhaps is proving its uniqueness. This is formulated as a conjecture of Łuczak and Peled in [Reference Łuczak and Peled12].
$Y_d(n, p)$
seems to be quite a difficult problem without obvious tools to approach it. More tractable perhaps is proving its uniqueness. This is formulated as a conjecture of Łuczak and Peled in [Reference Łuczak and Peled12].
Conjecture 1 (Łuczak and Peled [Reference Łuczak and Peled12]). For every
![]() $d \geq 2$
and
$d \geq 2$
and
![]() $p = p(n)$
such that
$p = p(n)$
such that
![]() $|np - c_d|$
is bounded away from 0,
$|np - c_d|$
is bounded away from 0,
![]() $H_{d - 1}(Y_d(n, p))$
is torsion-free asymptotically almost surely.
$H_{d - 1}(Y_d(n, p))$
is torsion-free asymptotically almost surely.
We point out that for
![]() $Y \sim Y_d(n, p)$
,
$Y \sim Y_d(n, p)$
,
![]() $H_{d - 1}(Y)$
a.a.s. does not vanish until
$H_{d - 1}(Y)$
a.a.s. does not vanish until
![]() $p = \frac{d \log n}{n}$
. This result was proved for fixed field coefficients in [Reference Linial and Meshulam10, Reference Meshulam and Wallach13], and for integer coefficients in the
$p = \frac{d \log n}{n}$
. This result was proved for fixed field coefficients in [Reference Linial and Meshulam10, Reference Meshulam and Wallach13], and for integer coefficients in the
![]() $d = 2$
case in [Reference Łuczak and Peled12] and in the general case in [Reference Newman and Paquette16]. Thus Conjecture 1 would provide a probability regime where
$d = 2$
case in [Reference Łuczak and Peled12] and in the general case in [Reference Newman and Paquette16]. Thus Conjecture 1 would provide a probability regime where
![]() $H_{d - 1}(Y)$
is nonvanishing and torsion-free.
$H_{d - 1}(Y)$
is nonvanishing and torsion-free.
In light of this conjecture and the comparison between random matrices over
![]() $\mathbb{Z}/2\mathbb{Z}$
with
$\mathbb{Z}/2\mathbb{Z}$
with
![]() $(d + 1)$
1’s in every row and
$(d + 1)$
1’s in every row and
![]() $Y_d(n, p)$
, we prove the following as our main theorem.
$Y_d(n, p)$
, we prove the following as our main theorem.
Theorem 2.
For any
![]() $k \geq 3$
, if
$k \geq 3$
, if
![]() $p = \omega \!\left(\frac{1}{n^{k - 1}}\right)$
then the cokernel of
$p = \omega \!\left(\frac{1}{n^{k - 1}}\right)$
then the cokernel of
![]() $M(\mathcal{H})$
for
$M(\mathcal{H})$
for
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely is torsion-free.
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely is torsion-free.
We remark also that the absence of torsion far below the phase transition, that is, for
![]() $p = o(1/n^{k - 1})$
, follows from facts about the 2-core of
$p = o(1/n^{k - 1})$
, follows from facts about the 2-core of
![]() $\mathcal{H}_k(n, p)$
. Recall that the 2-core of a hypergraph
$\mathcal{H}_k(n, p)$
. Recall that the 2-core of a hypergraph
![]() $\mathcal{H}$
is the hypergraph
$\mathcal{H}$
is the hypergraph
![]() $\mathcal{H'}$
obtained by successively deleting vertices (and hyperedges containing them) belonging to fewer than two hyperedges. Note that if
$\mathcal{H'}$
obtained by successively deleting vertices (and hyperedges containing them) belonging to fewer than two hyperedges. Note that if
![]() $\mathcal{H}$
is a
$\mathcal{H}$
is a
![]() $k$
-uniform hypergraph and
$k$
-uniform hypergraph and
![]() $v \in \mathcal{H}$
is contained in exactly one hyperedge
$v \in \mathcal{H}$
is contained in exactly one hyperedge
![]() $e$
then deleting
$e$
then deleting
![]() $v$
and
$v$
and
![]() $e$
from
$e$
from
![]() $\mathcal{H}$
does not change
$\mathcal{H}$
does not change
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
. On the other hand if
${\mathrm{coker}}(M(\mathcal{H}))$
. On the other hand if
![]() $v \in \mathcal{H}$
does not belong to any hyperedges at all, then deleting
$v \in \mathcal{H}$
does not belong to any hyperedges at all, then deleting
![]() $v$
from
$v$
from
![]() $\mathcal{H}$
removes a
$\mathcal{H}$
removes a
![]() $\mathbb{Z}$
factor from
$\mathbb{Z}$
factor from
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
. Therefore the torsion part of
${\mathrm{coker}}(M(\mathcal{H}))$
. Therefore the torsion part of
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
is the torsion part of
${\mathrm{coker}}(M(\mathcal{H}))$
is the torsion part of
![]() ${\mathrm{coker}}(M(\mathcal{H}'))$
where
${\mathrm{coker}}(M(\mathcal{H}'))$
where
![]() $\mathcal{H}'$
is the 2-core of
$\mathcal{H}'$
is the 2-core of
![]() $\mathcal{H}$
.
$\mathcal{H}$
.
One of the main results of a paper of Molloy [Reference Molloy15] establishes the sharp phase transition for the property that
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
for
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
for
![]() $k \geq 3$
has a nontrivial 2-core to be
$k \geq 3$
has a nontrivial 2-core to be
![]() $\gamma _k/n^{k - 1}$
for an explicit constant
$\gamma _k/n^{k - 1}$
for an explicit constant
![]() $\gamma _k$
. In fact the threshold that he establishes for this property is fundamentally the same as the threshold for
$\gamma _k$
. In fact the threshold that he establishes for this property is fundamentally the same as the threshold for
![]() $d$
-collapsibility in the Linial–Meshulam model established by [Reference Aronshtam and Linial1, Reference Aronshtam, Linial, Łuczak and Meshulam3] furthering the analogy between
$d$
-collapsibility in the Linial–Meshulam model established by [Reference Aronshtam and Linial1, Reference Aronshtam, Linial, Łuczak and Meshulam3] furthering the analogy between
![]() $Y_d(n, c/n)$
and
$Y_d(n, c/n)$
and
![]() $M(\mathcal{H}_k(n, c/n^{k - 1}))$
. Because of Molloy’s result about the 2-core and the connection between the 2-core and the torsion part of the cokernel we immediately have the following.
$M(\mathcal{H}_k(n, c/n^{k - 1}))$
. Because of Molloy’s result about the 2-core and the connection between the 2-core and the torsion part of the cokernel we immediately have the following.
Proposition 3.
For
![]() $k \geq 3$
, if
$k \geq 3$
, if
![]() $p = o\!\left(\frac{1}{n^{k - 1}}\right)$
then the cokernel of
$p = o\!\left(\frac{1}{n^{k - 1}}\right)$
then the cokernel of
![]() $M(\mathcal{H})$
if
$M(\mathcal{H})$
if
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely is torsion-free.
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely is torsion-free.
Also because of the comparison between
![]() $Y_d(n, p)$
and
$Y_d(n, p)$
and
![]() $M(\mathcal{H}_k(n, p))$
we prove the following analogue to the homology vanishing threshold in our random matrix model. This proof will follow immediately from Theorem 2 and a result about the
$M(\mathcal{H}_k(n, p))$
we prove the following analogue to the homology vanishing threshold in our random matrix model. This proof will follow immediately from Theorem 2 and a result about the
![]() $\mathbb{Z}/2\mathbb{Z}$
version of the random matrix model from [Reference Cooper, Frieze and Pegden6].
$\mathbb{Z}/2\mathbb{Z}$
version of the random matrix model from [Reference Cooper, Frieze and Pegden6].
Theorem 4.
For any
![]() $k \geq 3$
, if
$k \geq 3$
, if
![]() $p = \frac{c \log n}{n^{k - 1}}$
then for
$p = \frac{c \log n}{n^{k - 1}}$
then for
![]() $c \lt k!$
the cokernel of
$c \lt k!$
the cokernel of
![]() $M(\mathcal{H})$
for
$M(\mathcal{H})$
for
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely has free rank at least 1 when
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely has free rank at least 1 when
![]() $k$
is odd and at least 2 when
$k$
is odd and at least 2 when
![]() $k$
is even, while for
$k$
is even, while for
![]() $c \gt k!$
the cokernel of
$c \gt k!$
the cokernel of
![]() $M(\mathcal{H})$
for
$M(\mathcal{H})$
for
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely is
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
asymptotically almost surely is
![]() $0$
if
$0$
if
![]() $k$
is odd and is
$k$
is odd and is
![]() $\mathbb{Z}$
if
$\mathbb{Z}$
if
![]() $k$
is even.
$k$
is even.
Note that Theorems 2 and 4 implies that there is a probability regime where
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
is torsion-free, but also nontrivial.
${\mathrm{coker}}(M(\mathcal{H}))$
is torsion-free, but also nontrivial.
2. Outline of the proof of Theorem 2
Since the cokernel of an
![]() $n \times m$
matrix
$n \times m$
matrix
![]() $M$
is
$M$
is
![]() $\mathbb{Z}^n/\text{Im}(M)$
, a torsion element for
$\mathbb{Z}^n/\text{Im}(M)$
, a torsion element for
![]() ${\mathrm{coker}}(M)$
is an integer vector
${\mathrm{coker}}(M)$
is an integer vector
![]() $w$
so that
$w$
so that
![]() $w$
is not in the image of
$w$
is not in the image of
![]() $M$
but
$M$
but
![]() $tw$
is in the image of
$tw$
is in the image of
![]() $M$
for some
$M$
for some
![]() $t \geq 2$
. Obviously it suffices to rule out
$t \geq 2$
. Obviously it suffices to rule out
![]() $q$
-torsion over all primes
$q$
-torsion over all primes
![]() $q$
, that is, to show that for all primes
$q$
, that is, to show that for all primes
![]() $q$
there is never an integer vector
$q$
there is never an integer vector
![]() $w$
so that
$w$
so that
![]() $qw \in \text{Im}(M)$
but
$qw \in \text{Im}(M)$
but
![]() $w \notin \text{Im}(M)$
, however there is an important subtlety. We need to show that in the probability regime considered we can bound the probability that there is
$w \notin \text{Im}(M)$
, however there is an important subtlety. We need to show that in the probability regime considered we can bound the probability that there is
![]() $q$
-torsion simultaneously over all primes
$q$
-torsion simultaneously over all primes
![]() $q$
. It would not be enough to fix
$q$
. It would not be enough to fix
![]() $q$
and show that the probability of
$q$
and show that the probability of
![]() $q$
-torsion is
$q$
-torsion is
![]() $o(1)$
. Such an approach would leave open the possibility that there is
$o(1)$
. Such an approach would leave open the possibility that there is
![]() $q(n)$
-torsion in our random model for some sequence of primes
$q(n)$
-torsion in our random model for some sequence of primes
![]() $q(n)$
growing with
$q(n)$
growing with
![]() $n$
.
$n$
.
We first state the key lemmas to sketch out the arguments. It turns out to be easier to rule out torsion in
![]() ${\mathrm{coker}}(M^T)$
rather than directly ruling out torsion for
${\mathrm{coker}}(M^T)$
rather than directly ruling out torsion for
![]() ${\mathrm{coker}}(M)$
. This is similar to how [Reference Linial and Meshulam10, Reference Łuczak and Peled12, Reference Meshulam and Wallach13, Reference Newman and Paquette16] prove cohomology vanishing theorems rather than directly proving homology vanishing theorems. This formulation is equivalent since the torsion coefficients of an integer matrix come from its Smith normal form; the torsion part of
${\mathrm{coker}}(M)$
. This is similar to how [Reference Linial and Meshulam10, Reference Łuczak and Peled12, Reference Meshulam and Wallach13, Reference Newman and Paquette16] prove cohomology vanishing theorems rather than directly proving homology vanishing theorems. This formulation is equivalent since the torsion coefficients of an integer matrix come from its Smith normal form; the torsion part of
![]() ${\mathrm{coker}}(M^T)$
is the same as the torsion part of
${\mathrm{coker}}(M^T)$
is the same as the torsion part of
![]() ${\mathrm{coker}}(M)$
for any matrix.
${\mathrm{coker}}(M)$
for any matrix.
The idea of the proof is to show that with high probability there are no
![]() $w$
,
$w$
,
![]() $v$
,
$v$
,
![]() $q$
so that
$q$
so that
![]() $M^Tv = qw$
with
$M^Tv = qw$
with
![]() $q$
prime,
$q$
prime,
![]() $v \notin (q\mathbb{Z})^n$
, and
$v \notin (q\mathbb{Z})^n$
, and
![]() $w \notin \text{Im}(M^T)$
. The argument splits depending on the size of the support of
$w \notin \text{Im}(M^T)$
. The argument splits depending on the size of the support of
![]() $v$
. The first key lemma has to do with the case that the support of
$v$
. The first key lemma has to do with the case that the support of
![]() $v$
is small. Here we introduce the notation
$v$
is small. Here we introduce the notation
![]() $M_S$
for
$M_S$
for
![]() $S$
a subset of the columns of
$S$
a subset of the columns of
![]() $M$
to be the submatrix obtained by restricting
$M$
to be the submatrix obtained by restricting
![]() $M$
to the columns belonging to
$M$
to the columns belonging to
![]() $S$
.
$S$
.
Lemma 5.
Fix
![]() $\delta \in (0, 1)$
then for
$\delta \in (0, 1)$
then for
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
with
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
with
![]() $p = \omega (1/n^{k - 1})$
asymptotically almost surely for every set
$p = \omega (1/n^{k - 1})$
asymptotically almost surely for every set
![]() $S \subseteq [n]$
with
$S \subseteq [n]$
with
![]() $|S| \lt \delta n$
,
$|S| \lt \delta n$
,
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M^T_S) ={\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M^T_S)$
for every prime
${\mathrm{rank}}_{\mathbb{Q}}(M^T_S) ={\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M^T_S)$
for every prime
![]() $q$
where
$q$
where
![]() $M = M(\mathcal{H})$
.
$M = M(\mathcal{H})$
.
For the case that the support of
![]() $v$
is large the argument splits depending on the parity of
$v$
is large the argument splits depending on the parity of
![]() $k$
. For the case that
$k$
. For the case that
![]() $k$
is odd the argument is a bit more straightforward. The issue when
$k$
is odd the argument is a bit more straightforward. The issue when
![]() $k$
is even is that the row sum along every row of
$k$
is even is that the row sum along every row of
![]() $M^T$
is zero, so the all-ones vector is always in the kernel of
$M^T$
is zero, so the all-ones vector is always in the kernel of
![]() $M^T$
which makes the argument slightly more difficult. The lemma to handle the odd case is the following. Note that here we use
$M^T$
which makes the argument slightly more difficult. The lemma to handle the odd case is the following. Note that here we use
![]() $\mathcal{H}_k(n, m)$
the uniform distribution on
$\mathcal{H}_k(n, m)$
the uniform distribution on
![]() $k$
-uniform hypergraphs with exactly
$k$
-uniform hypergraphs with exactly
![]() $m$
hyperedges.
$m$
hyperedges.
Lemma 6.
For any
![]() $k \geq 3$
odd,
$k \geq 3$
odd,
![]() $\delta \gt 0$
, and
$\delta \gt 0$
, and
![]() $c = c(k, \delta )$
a sufficiently large constant there exists
$c = c(k, \delta )$
a sufficiently large constant there exists
![]() $C = C(k, c, \delta ) \gt \log\!(k)$
so that for any prime
$C = C(k, c, \delta ) \gt \log\!(k)$
so that for any prime
![]() $q$
the probability that
$q$
the probability that
![]() $\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
for
$\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
for
![]() $M = M(\mathcal{H})$
,
$M = M(\mathcal{H})$
,
![]() $\mathcal{H}_k(n, cn)$
contains a vector of support size at least
$\mathcal{H}_k(n, cn)$
contains a vector of support size at least
![]() $\delta n$
is at most
$\delta n$
is at most
![]() $e^{-Cn}$
.
$e^{-Cn}$
.
Note here that the
![]() $C$
in the statement does not depend on
$C$
in the statement does not depend on
![]() $q$
. This is important because the following lemma tells us that we only have to consider exponentially many primes. This lemma is well known, and it seem that the earliest reference to it is a paper of Soulé [Reference Soulé18]. It appears in papers about vanishing homology theorems for random complexes. In particular, it appears with proof as Claim 2 of [Reference Newman and Paquette16].
$q$
. This is important because the following lemma tells us that we only have to consider exponentially many primes. This lemma is well known, and it seem that the earliest reference to it is a paper of Soulé [Reference Soulé18]. It appears in papers about vanishing homology theorems for random complexes. In particular, it appears with proof as Claim 2 of [Reference Newman and Paquette16].
Lemma 7.
If
![]() $M$
is an integer matrix with
$M$
is an integer matrix with
![]() $n$
columns so that each column of
$n$
columns so that each column of
![]() $M$
has Euclidean norm at most
$M$
has Euclidean norm at most
![]() $t$
then the torsion part of
$t$
then the torsion part of
![]() ${\mathrm{coker}}(M)$
has size at most
${\mathrm{coker}}(M)$
has size at most
![]() $t^n$
.
$t^n$
.
With Lemmas 5–7 we can prove Theorem 2 for
![]() $k$
odd.
$k$
odd.
Proof of Theorem
2 for odd k. For
![]() $p = \omega (1/n^{k - 1} )$
we bound the probability that
$p = \omega (1/n^{k - 1} )$
we bound the probability that
![]() $M \;:\!=\; M(\mathcal{H})$
has cokernel with torsion when
$M \;:\!=\; M(\mathcal{H})$
has cokernel with torsion when
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
. If
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
. If
![]() ${\mathrm{coker}}(M)$
has torsion then it has
${\mathrm{coker}}(M)$
has torsion then it has
![]() $q$
-torsion for some prime
$q$
-torsion for some prime
![]() $q \leq \sqrt{k}^n$
. Moreover if
$q \leq \sqrt{k}^n$
. Moreover if
![]() $M$
has
$M$
has
![]() $q$
-torsion then so does
$q$
-torsion then so does
![]() ${\mathrm{coker}}(M^T)$
, so in that case there exists a vector
${\mathrm{coker}}(M^T)$
, so in that case there exists a vector
![]() $v$
so that
$v$
so that
![]() $M^Tv = qw$
for
$M^Tv = qw$
for
![]() $w$
an integer vector not in the image of
$w$
an integer vector not in the image of
![]() $M^T$
and
$M^T$
and
![]() $v \notin (q\mathbb{Z})^n$
. In this case
$v \notin (q\mathbb{Z})^n$
. In this case
![]() $v \pmod q$
is a nontrivial vector in
$v \pmod q$
is a nontrivial vector in
![]() $\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
. By Lemma 6 and a union bound over all
$\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
. By Lemma 6 and a union bound over all
![]() $\sqrt{k}^n$
primes under consideration we see that with high probability, there is no vector in
$\sqrt{k}^n$
primes under consideration we see that with high probability, there is no vector in
![]() $\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
with support size larger than
$\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
with support size larger than
![]() $n/2$
for any prime
$n/2$
for any prime
![]() $q \leq \sqrt{k}^n$
. Indeed letting
$q \leq \sqrt{k}^n$
. Indeed letting
![]() $T_q$
denote the event that there is a vector
$T_q$
denote the event that there is a vector
![]() $v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
with support size at least
$v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
with support size at least
![]() $n/2$
and taking union bound over all primes smaller than
$n/2$
and taking union bound over all primes smaller than
![]() $\sqrt{k}^n$
we find the probability that there is
$\sqrt{k}^n$
we find the probability that there is
![]() $v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
of large support for some prime
$v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
of large support for some prime
![]() $q$
is at most
$q$
is at most
 \begin{eqnarray*} \mathbb{P}\left (\bigcup _{q \leq \sqrt{k}^n, q \text{ prime }} T_q\right ) &\leq & \mathbb{P}\left (\bigcup _{q \leq \sqrt{k}^n, q \text{ prime }} T_q \middle | |E(\mathcal{H})| \gt cn\right ) + \mathbb{P}(|E(\mathcal{H})| \leq cn)\\[5pt] &\leq & \sum _{q \leq \sqrt{k}^n, q \text{ prime }} \mathbb{P}(T_q | |E(H)| \gt cn) + \mathbb{P}(|E(H)| \leq cn) \end{eqnarray*}
\begin{eqnarray*} \mathbb{P}\left (\bigcup _{q \leq \sqrt{k}^n, q \text{ prime }} T_q\right ) &\leq & \mathbb{P}\left (\bigcup _{q \leq \sqrt{k}^n, q \text{ prime }} T_q \middle | |E(\mathcal{H})| \gt cn\right ) + \mathbb{P}(|E(\mathcal{H})| \leq cn)\\[5pt] &\leq & \sum _{q \leq \sqrt{k}^n, q \text{ prime }} \mathbb{P}(T_q | |E(H)| \gt cn) + \mathbb{P}(|E(H)| \leq cn) \end{eqnarray*}
where
![]() $c$
is some sufficiently large constant for the assumptions of Lemma 6 to hold. By a standard coupling argument between
$c$
is some sufficiently large constant for the assumptions of Lemma 6 to hold. By a standard coupling argument between
![]() $\mathcal{H}_k(n, cn)$
and
$\mathcal{H}_k(n, cn)$
and
![]() $\mathcal{H}_{k}(n, p)$
for
$\mathcal{H}_{k}(n, p)$
for
![]() $p = \omega (1/n^{k - 1})$
, we apply Lemma 6 to conclude that each term in the sum over at most
$p = \omega (1/n^{k - 1})$
, we apply Lemma 6 to conclude that each term in the sum over at most
![]() $\sqrt{k}^n$
primes is at most
$\sqrt{k}^n$
primes is at most
![]() $\exp\!(\!-\!Cn)$
for
$\exp\!(\!-\!Cn)$
for
![]() $C \gt \log\!(k)$
. Thus the large sum is at most
$C \gt \log\!(k)$
. Thus the large sum is at most
![]() $\exp\!(\!-\!n\log\!(k)/2)$
and the last term is
$\exp\!(\!-\!n\log\!(k)/2)$
and the last term is
![]() $o(1)$
since the number of hyperedges of
$o(1)$
since the number of hyperedges of
![]() $\mathcal{H}$
is distributed as a binomial with mean
$\mathcal{H}$
is distributed as a binomial with mean
![]() $\omega (n)$
.
$\omega (n)$
.
We can assume now that the vector
![]() $v$
with
$v$
with
![]() $M^Tv = qw$
has support size (over
$M^Tv = qw$
has support size (over
![]() $\mathbb{Z}/q\mathbb{Z}$
) at most
$\mathbb{Z}/q\mathbb{Z}$
) at most
![]() $n/2$
. We know however that with high probability
$n/2$
. We know however that with high probability
![]() $M^T$
satisfies the assumption of Lemma 5 with
$M^T$
satisfies the assumption of Lemma 5 with
![]() $\delta = 1/2$
. In this case then taking
$\delta = 1/2$
. In this case then taking
![]() $S$
to be the support of
$S$
to be the support of
![]() $v$
over
$v$
over
![]() $\mathbb{Z}/q\mathbb{Z}$
, we see that
$\mathbb{Z}/q\mathbb{Z}$
, we see that
![]() ${\mathrm{rank}}_{\mathbb{Q}}((M^T)_S) ={\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}((M^T)_S)$
. Therefore
${\mathrm{rank}}_{\mathbb{Q}}((M^T)_S) ={\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}((M^T)_S)$
. Therefore
![]() ${\mathrm{coker}}((M^T)_S)$
is
${\mathrm{coker}}((M^T)_S)$
is
![]() $q$
-torsion-free. As
$q$
-torsion-free. As
![]() $S$
is the support of
$S$
is the support of
![]() $v$
over
$v$
over
![]() $\mathbb{Z}/q\mathbb{Z}$
,
$\mathbb{Z}/q\mathbb{Z}$
,
![]() $v = v_1 + qv_2$
where
$v = v_1 + qv_2$
where
![]() ${\mathrm{supp}}(v_1) = S$
, we have that
${\mathrm{supp}}(v_1) = S$
, we have that
![]() $qw = M^T(v_1 + qv_2) \in{\mathrm{coker}}((M^T))$
, so
$qw = M^T(v_1 + qv_2) \in{\mathrm{coker}}((M^T))$
, so
![]() $M^T(v_1) = qw_1$
for some vector
$M^T(v_1) = qw_1$
for some vector
![]() $w_1$
. As
$w_1$
. As
![]() $v_1$
is supported on
$v_1$
is supported on
![]() $S$
and
$S$
and
![]() ${\mathrm{coker}}((M^T)_S)$
is torsion-free there is some integer vector
${\mathrm{coker}}((M^T)_S)$
is torsion-free there is some integer vector
![]() $u$
supported on
$u$
supported on
![]() $S$
with
$S$
with
![]() $M^Tu = w_1$
and so
$M^Tu = w_1$
and so
![]() $M^T(u + v_2) = w$
contradicting the choice of
$M^T(u + v_2) = w$
contradicting the choice of
![]() $w$
as a torsion element of
$w$
as a torsion element of
![]() ${\mathrm{coker}}(M^T)$
.
${\mathrm{coker}}(M^T)$
.
The proof when
![]() $k$
is even makes use of a definition we introduce later, so we save the proof for the even case for the end.
$k$
is even makes use of a definition we introduce later, so we save the proof for the even case for the end.
3. Vectors with small support
Here we prove Lemma 5. Toward that goal we start with the following definition.
Definition 8. Let
![]() $M$
be an integer matrix, a subset
$M$
be an integer matrix, a subset
![]() $S$
of the columns of
$S$
of the columns of
![]() $M$
is said to be a torsion cocycle provided that there exists a prime
$M$
is said to be a torsion cocycle provided that there exists a prime
![]() $q$
so that
$q$
so that
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M_S) \gt{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_S)$
. A minimal torsion cocycle is an inclusion-minimal set of columns
${\mathrm{rank}}_{\mathbb{Q}}(M_S) \gt{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_S)$
. A minimal torsion cocycle is an inclusion-minimal set of columns
![]() $S$
which is a torsion cocycle.
$S$
which is a torsion cocycle.
The name torsion cocycle comes from the fact that our proof of the main theorem here is an adaptation of the cocycle counting argument from proofs of homology vanishing theorems in [Reference Linial and Meshulam10, Reference Meshulam and Wallach13, Reference Newman and Paquette16]. The following claim about minimal torsion cocycles is easy to prove and sets up a sub-hypergraph inclusion problem to rule out small torsion cocycles and prove Lemma 5.
Claim 9.
If
![]() $S$
is a minimal torsion cocycle of a matrix
$S$
is a minimal torsion cocycle of a matrix
![]() $M$
, then
$M$
, then
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M_S) = |S|$
. Moreover
${\mathrm{rank}}_{\mathbb{Q}}(M_S) = |S|$
. Moreover
![]() $M_S$
cannot have a row which has
$M_S$
cannot have a row which has
![]() $|S| - 1$
entries equal to zero and the remaining entry equal to
$|S| - 1$
entries equal to zero and the remaining entry equal to
![]() $1$
or to
$1$
or to
![]() $-1$
.
$-1$
.
Proof. Suppose that
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M_S) \lt |S|$
. Let
${\mathrm{rank}}_{\mathbb{Q}}(M_S) \lt |S|$
. Let
![]() $U \subsetneq S$
be a maximal collection of linearly independent columns of
$U \subsetneq S$
be a maximal collection of linearly independent columns of
![]() $M_S$
over
$M_S$
over
![]() $\mathbb{Q}$
. Since
$\mathbb{Q}$
. Since
![]() $S$
is a torsion cocycle there exists a prime
$S$
is a torsion cocycle there exists a prime
![]() $q$
so that
$q$
so that
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M_S) \gt{\mathrm{rank}}_{\mathbb{Z}/q/\mathbb{Z}}(M_S)$
. By minimality of
${\mathrm{rank}}_{\mathbb{Q}}(M_S) \gt{\mathrm{rank}}_{\mathbb{Z}/q/\mathbb{Z}}(M_S)$
. By minimality of
![]() $S$
,
$S$
,
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M_U) ={\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_U)$
. On the other hand, we have
${\mathrm{rank}}_{\mathbb{Q}}(M_U) ={\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_U)$
. On the other hand, we have
 \begin{eqnarray*}{\mathrm{rank}}_{\mathbb{Q}}(M_U) &=&{\mathrm{rank}}_{\mathbb{Q}}(M_S) \\[5pt] &\gt &{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_S) \\[5pt] &\geq &{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_U). \end{eqnarray*}
\begin{eqnarray*}{\mathrm{rank}}_{\mathbb{Q}}(M_U) &=&{\mathrm{rank}}_{\mathbb{Q}}(M_S) \\[5pt] &\gt &{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_S) \\[5pt] &\geq &{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_U). \end{eqnarray*}
Thus, we reach a contradiction and finish the proof of the first part of the claim.
For the second part, we observe that if
![]() $z$
is a row of
$z$
is a row of
![]() $M_S$
so that the
$M_S$
so that the
![]() $i$
th entry of
$i$
th entry of
![]() $z$
is
$z$
is
![]() $\pm 1$
and all other entries of
$\pm 1$
and all other entries of
![]() $z$
are
$z$
are
![]() $0$
then clearly over any field column
$0$
then clearly over any field column
![]() $i$
of
$i$
of
![]() $M_S$
is outside the span of all other columns of
$M_S$
is outside the span of all other columns of
![]() $M_S$
. Thus, deleting
$M_S$
. Thus, deleting
![]() $i$
from
$i$
from
![]() $S$
drops the rank of
$S$
drops the rank of
![]() $M_S$
over any field by 1. Thus
$M_S$
over any field by 1. Thus
![]() when
when
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M_S) \gt{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_S)$
as both ranks drop by one. However this contradicts minimality.
${\mathrm{rank}}_{\mathbb{Q}}(M_S) \gt{\mathrm{rank}}_{\mathbb{Z}/q\mathbb{Z}}(M_S)$
as both ranks drop by one. However this contradicts minimality.
By the claim, we have that in any set of columns
![]() $S \subseteq [n]$
of
$S \subseteq [n]$
of
![]() $M^T$
which form a minimal torsion cocycle there must be at least
$M^T$
which form a minimal torsion cocycle there must be at least
![]() $|S|$
nonzero rows in
$|S|$
nonzero rows in
![]() $M^T_S$
. Otherwise the (row) rank of
$M^T_S$
. Otherwise the (row) rank of
![]() $M^T_S$
over
$M^T_S$
over
![]() $\mathbb{Q}$
would be smaller than
$\mathbb{Q}$
would be smaller than
![]() $|S|$
. As the columns of
$|S|$
. As the columns of
![]() $M^T$
are indexed by vertices of
$M^T$
are indexed by vertices of
![]() $\mathcal{H}$
and the rows are indexed by hyperedges of
$\mathcal{H}$
and the rows are indexed by hyperedges of
![]() $\mathcal{H}$
, for
$\mathcal{H}$
, for
![]() $S$
the set of
$S$
the set of
![]() $t$
vertices corresponding to the minimal torsion cocycle we have by the two parts of Claim 9:
$t$
vertices corresponding to the minimal torsion cocycle we have by the two parts of Claim 9:
-
1. There are at least
 $t$
hyperedges in the random hypergraph which involve at least one vertex of
$t$
hyperedges in the random hypergraph which involve at least one vertex of
 $S$
, but
$S$
, but -
2. no hyperedge contains exactly one vertex of
 $S$
.
$S$
.
We use a linearity of expectation argument to bound the probability that
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
for
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
for
![]() $p = \omega (1/n^{k - 1})$
has a small subset of vertices
$p = \omega (1/n^{k - 1})$
has a small subset of vertices
![]() $S$
which satisfies conditions (1) and (2) above.
$S$
which satisfies conditions (1) and (2) above.
Lemma 10.
Fix
![]() $\delta \in (0, 1)$
and take
$\delta \in (0, 1)$
and take
![]() $p = \omega (1/n^{k - 1})$
. With high probability
$p = \omega (1/n^{k - 1})$
. With high probability
![]() $\mathcal{H} \sim \mathcal{H}_k(n, p)$
does not contain a subset of vertices
$\mathcal{H} \sim \mathcal{H}_k(n, p)$
does not contain a subset of vertices
![]() $S$
with
$S$
with
![]() $|S| \leq \delta n$
satisfying both of the following:
$|S| \leq \delta n$
satisfying both of the following:
-
• There are at least
 $|S|$
hyperedges that intersect
$|S|$
hyperedges that intersect
 $S$
, but
$S$
, but
-
• no hyperedge intersects
 $S$
exactly once.
$S$
exactly once.
Proof. We prove this by counting the expected number of subsets
![]() $S$
satisfying both of the conditions. Let
$S$
satisfying both of the conditions. Let
![]() $t$
denote the size of
$t$
denote the size of
![]() $S$
. For each
$S$
. For each
![]() $1 \leq t \leq \delta n$
there are
$1 \leq t \leq \delta n$
there are
![]() $\binom{n}{t}$
ways to pick
$\binom{n}{t}$
ways to pick
![]() $S$
. From here we have to choose at least
$S$
. From here we have to choose at least
![]() $t$
hyperedges that intersect
$t$
hyperedges that intersect
![]() $S$
in at least 2 vertices to be included. The number of hyperedges that intersect
$S$
in at least 2 vertices to be included. The number of hyperedges that intersect
![]() $S$
in at least 2 vertices is
$S$
in at least 2 vertices is
 \begin{equation*}\sum _{i = 0}^{k -2} \binom {n - t}{i} \binom {t}{k - i} \leq \sum _{i = 0}^{k - 2} n^i t^{k - i} .\end{equation*}
\begin{equation*}\sum _{i = 0}^{k -2} \binom {n - t}{i} \binom {t}{k - i} \leq \sum _{i = 0}^{k - 2} n^i t^{k - i} .\end{equation*}
And from this set, we choose at least
![]() $t$
hyperedges to be included. Next, we have to guarantee that all hyperedges that intersect
$t$
hyperedges to be included. Next, we have to guarantee that all hyperedges that intersect
![]() $S$
in only one place are excluded. The number of hyperedges that meet
$S$
in only one place are excluded. The number of hyperedges that meet
![]() $S$
in exactly one vertex is
$S$
in exactly one vertex is
Putting this all together the number of expected number of sets
![]() $S$
that satisfy the conditions we want to avoid is at most
$S$
that satisfy the conditions we want to avoid is at most
 \begin{eqnarray*} \sum _{t = 1}^{\delta n} \binom{n}{t} e^t \left ( \frac{\sum _{i = 0}^{k -2} n^i t^{k - i}}{t} \right )^t p^t \exp\!\left (\!-p \binom{n - t}{k - 1}\right )^t. \end{eqnarray*}
\begin{eqnarray*} \sum _{t = 1}^{\delta n} \binom{n}{t} e^t \left ( \frac{\sum _{i = 0}^{k -2} n^i t^{k - i}}{t} \right )^t p^t \exp\!\left (\!-p \binom{n - t}{k - 1}\right )^t. \end{eqnarray*}
Taking
![]() $p = f/n^{k - 1}$
with
$p = f/n^{k - 1}$
with
![]() $f \;:\!=\; f(n) \rightarrow \infty$
arbitrarily slowly, we have the above is at most
$f \;:\!=\; f(n) \rightarrow \infty$
arbitrarily slowly, we have the above is at most
 \begin{eqnarray*} \sum _{t = 1}^{\delta n} \frac{n^t e^{2t}}{t^t} \left ( \sum _{i = 0}^{k -2} n^i t^{k - i - 1} \right )^t \left (\frac{f}{n^{k - 1}}\right )^t \exp\!\left (-(f/n^{k - 1}) \frac{(1 - \delta )^{k - 1}n^{k - 1}}{(k - 1)^{k - 1}}\right )^t. \end{eqnarray*}
\begin{eqnarray*} \sum _{t = 1}^{\delta n} \frac{n^t e^{2t}}{t^t} \left ( \sum _{i = 0}^{k -2} n^i t^{k - i - 1} \right )^t \left (\frac{f}{n^{k - 1}}\right )^t \exp\!\left (-(f/n^{k - 1}) \frac{(1 - \delta )^{k - 1}n^{k - 1}}{(k - 1)^{k - 1}}\right )^t. \end{eqnarray*}
Thus for some positive constant
![]() $c = c_{k, \delta }$
that depends on
$c = c_{k, \delta }$
that depends on
![]() $k$
and
$k$
and
![]() $\delta$
, we have that the above sum is at most
$\delta$
, we have that the above sum is at most
 \begin{eqnarray*} \sum _{t = 1}^{\delta n} \left (e^2 n \sum _{i = 0}^{k - 2} n^i t^{k - i - 2} \right )^t \left (\frac{f}{n^{k - 1}}\right )^t \exp\!\left (-f c\right )^t &\leq & \sum _{t = 1}^{\delta n} \left (e^2 n^{2 - k} f\sum _{i = 0}^{k - 2} \delta ^{k - i - 2}n^{k - 2} \right )^t \exp\!\left (-f c\right )^t \\[5pt] &\leq & \sum _{t = 1}^{\delta n} \left ( e^2 (k - 1) f e^{-c f} \right )^t \end{eqnarray*}
\begin{eqnarray*} \sum _{t = 1}^{\delta n} \left (e^2 n \sum _{i = 0}^{k - 2} n^i t^{k - i - 2} \right )^t \left (\frac{f}{n^{k - 1}}\right )^t \exp\!\left (-f c\right )^t &\leq & \sum _{t = 1}^{\delta n} \left (e^2 n^{2 - k} f\sum _{i = 0}^{k - 2} \delta ^{k - i - 2}n^{k - 2} \right )^t \exp\!\left (-f c\right )^t \\[5pt] &\leq & \sum _{t = 1}^{\delta n} \left ( e^2 (k - 1) f e^{-c f} \right )^t \end{eqnarray*}
And this is
![]() $o(1)$
as long as
$o(1)$
as long as
![]() $f$
tends to infinity. Thus by Markov’s inequality we have the lemma.
$f$
tends to infinity. Thus by Markov’s inequality we have the lemma.
Lemma 5 follows immediately from Claim 9 and Lemma 10.
Remark 11. Lemma 10 turns out to be the only part of the proof of Theorem 2 where we use
![]() $p = \omega (1/n^{k - 1})$
and where it could not be replaced with
$p = \omega (1/n^{k - 1})$
and where it could not be replaced with
![]() $p = C/n^{k - 1}$
with
$p = C/n^{k - 1}$
with
![]() $C = C(k)$
a large constant. While the main theorem still ought to hold for
$C = C(k)$
a large constant. While the main theorem still ought to hold for
![]() $p = C/n^{k - 1}$
, the first moment argument in Lemma 10 does not work in this case. As an illustration of what goes wrong, let’s just consider the
$p = C/n^{k - 1}$
, the first moment argument in Lemma 10 does not work in this case. As an illustration of what goes wrong, let’s just consider the
![]() $k = 3$
case. A set
$k = 3$
case. A set
![]() $S$
of three vertices so that each pair is contained in at least one hyperedge with the third vertex being outside of
$S$
of three vertices so that each pair is contained in at least one hyperedge with the third vertex being outside of
![]() $S$
, but no hyperedge intersects
$S$
, but no hyperedge intersects
![]() $S$
exactly once is a configuration we want to rule out with Lemma 10. However the expected number of such configurations is at least:
$S$
exactly once is a configuration we want to rule out with Lemma 10. However the expected number of such configurations is at least:
but this has a constant, nonzero lower bound for
![]() $C$
fixed when
$C$
fixed when
![]() $n$
is large enough.
$n$
is large enough.
4. Vectors with large support
We turn our attention now to the proof of Lemma 6. As this proof is about
![]() $\mathcal{H}_k(n, m)$
we consider
$\mathcal{H}_k(n, m)$
we consider
![]() $\mathcal{H}_k(n, m)$
and the corresponding
$\mathcal{H}_k(n, m)$
and the corresponding
![]() $M(\mathcal{H})$
as a stochastic process obtained by adding the hyperedges of
$M(\mathcal{H})$
as a stochastic process obtained by adding the hyperedges of
![]() $\binom{[n]}{k}$
one at a time in random order. In order to prove Theorem 6 we want to find a lower bound on the probability that the dimension of the kernel of
$\binom{[n]}{k}$
one at a time in random order. In order to prove Theorem 6 we want to find a lower bound on the probability that the dimension of the kernel of
![]() $M^T$
drops as we add the random rows of
$M^T$
drops as we add the random rows of
![]() $M^T$
one at a time. The arguments here are similar to the coboundary expansion arguments found in [Reference Linial and Meshulam10, Reference Meshulam and Wallach13, Reference Newman and Paquette16] where a cocycle counting argument is applied to prove homology vanishing theorems in the Linial–Meshulam model. The idea of coboundary expansion is discussed in more detail in [Reference Dotterrer and Kahle7].
$M^T$
one at a time. The arguments here are similar to the coboundary expansion arguments found in [Reference Linial and Meshulam10, Reference Meshulam and Wallach13, Reference Newman and Paquette16] where a cocycle counting argument is applied to prove homology vanishing theorems in the Linial–Meshulam model. The idea of coboundary expansion is discussed in more detail in [Reference Dotterrer and Kahle7].
To set up our arguments, we introduce the following definition.
Definition 12. Take
![]() $V_{k, n}$
to be the set of vectors that can be column vectors of
$V_{k, n}$
to be the set of vectors that can be column vectors of
![]() $M(\mathcal{H})$
, that is,
$M(\mathcal{H})$
, that is,
![]() $V_{k, n}$
is the set of vectors in
$V_{k, n}$
is the set of vectors in
![]() $\mathbb{Z}^n$
with exactly
$\mathbb{Z}^n$
with exactly
![]() $k$
nonzero entries and the nonzero entries alternating as
$k$
nonzero entries and the nonzero entries alternating as
![]() $1,-1, 1, -1, \ldots$
. For
$1,-1, 1, -1, \ldots$
. For
![]() $k \geq 3$
,
$k \geq 3$
,
![]() $q$
prime, and
$q$
prime, and
![]() $v \in (\mathbb{Z}/q\mathbb{Z})^n$
let
$v \in (\mathbb{Z}/q\mathbb{Z})^n$
let
![]() $B_q(v)$
denote the set
$B_q(v)$
denote the set ![]() . We observe that for any matrix
. We observe that for any matrix
![]() $M$
with rows in
$M$
with rows in
![]() $V_{k, n}$
if
$V_{k, n}$
if
![]() $v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M)$
, and we add a row in
$v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M)$
, and we add a row in
![]() $V_{k, n}$
to it to create a new matrix
$V_{k, n}$
to it to create a new matrix
![]() $M'$
then
$M'$
then
![]() $v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M')$
if and only if the new row is outside of
$v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M')$
if and only if the new row is outside of
![]() $B_q(v)$
.
$B_q(v)$
.
We prove the following statement regarding
![]() $B_q(v)$
when
$B_q(v)$
when
![]() $k$
is odd. Those familiar with coboundary expansion will find this lemma and Lemma 16 analogous to Proposition 2.1 of [Reference Meshulam and Wallach13], although the proofs are quite different.
$k$
is odd. Those familiar with coboundary expansion will find this lemma and Lemma 16 analogous to Proposition 2.1 of [Reference Meshulam and Wallach13], although the proofs are quite different.
Lemma 13.
For
![]() $k$
odd there exists
$k$
odd there exists
![]() $\gamma \;:\!=\; \gamma (k) \gt 0$
so that for every prime
$\gamma \;:\!=\; \gamma (k) \gt 0$
so that for every prime
![]() $q$
and every vector
$q$
and every vector
![]() $v \in (\mathbb{Z}/q\mathbb{Z})^n$
,
$v \in (\mathbb{Z}/q\mathbb{Z})^n$
,
![]() $|B_q(v)| \geq \gamma |{\mathrm{supp}}(v)|^k$
.
$|B_q(v)| \geq \gamma |{\mathrm{supp}}(v)|^k$
.
In order to prove this lemma we introduce the following definition.
Definition 14. For
![]() $q$
a prime and
$q$
a prime and
![]() $\varepsilon \gt 0$
, we say that
$\varepsilon \gt 0$
, we say that
![]() $v \in (\mathbb{Z}/q\mathbb{Z})^n$
is
$v \in (\mathbb{Z}/q\mathbb{Z})^n$
is
![]() $\varepsilon$
-balanced provided every nonzero element of
$\varepsilon$
-balanced provided every nonzero element of
![]() $\mathbb{Z}/q\mathbb{Z}$
appears at most
$\mathbb{Z}/q\mathbb{Z}$
appears at most
![]() $\varepsilon |{\mathrm{supp}}(v)|$
times in
$\varepsilon |{\mathrm{supp}}(v)|$
times in
![]() $v$
.
$v$
.
With the definition of
![]() $\varepsilon$
-balanced the proof of Lemma 13 splits into two cases.
$\varepsilon$
-balanced the proof of Lemma 13 splits into two cases.
Proof of Lemma
13
. For a vector
![]() $v \in (\mathbb{Z}/q\mathbb{Z})^n$
we wish to bound from below the number of
$v \in (\mathbb{Z}/q\mathbb{Z})^n$
we wish to bound from below the number of
![]() $w \in V_{k, n}$
so that
$w \in V_{k, n}$
so that
![]() $w \cdot v \neq 0$
. With foresight into the calculations fix some positive
$w \cdot v \neq 0$
. With foresight into the calculations fix some positive
![]() $\varepsilon \lt \frac{(k - 1)!}{k^{k}}$
. We consider first the case that
$\varepsilon \lt \frac{(k - 1)!}{k^{k}}$
. We consider first the case that
![]() $v$
is
$v$
is
![]() $\varepsilon$
-balanced.
$\varepsilon$
-balanced.
If
![]() $v$
is
$v$
is
![]() $\varepsilon$
-balanced then there are at least
$\varepsilon$
-balanced then there are at least
vectors
![]() $w$
in
$w$
in
![]() $V_{k, n}$
over
$V_{k, n}$
over
![]() $\mathbb{Z}/q\mathbb{Z}$
so that
$\mathbb{Z}/q\mathbb{Z}$
so that
![]() $w \cdot v \neq 0$
. To see this we restrict only to those vectors
$w \cdot v \neq 0$
. To see this we restrict only to those vectors
![]() $w \in V_{k, n}$
so that
$w \in V_{k, n}$
so that
![]() ${\mathrm{supp}}(w) \subseteq{\mathrm{supp}}(v)$
; denote this set by
${\mathrm{supp}}(w) \subseteq{\mathrm{supp}}(v)$
; denote this set by
![]() $V_{k, n}^v$
. There are clearly (exactly)
$V_{k, n}^v$
. There are clearly (exactly)
![]() $\binom{|{\mathrm{supp}}(v)|}{k}$
vectors in
$\binom{|{\mathrm{supp}}(v)|}{k}$
vectors in
![]() $V_{k, n}^v$
. We claim that among these vectors at most
$V_{k, n}^v$
. We claim that among these vectors at most
![]() $\binom{|{\mathrm{supp}}(v)|}{k - 1} \varepsilon |{\mathrm{supp}}(v)|$
will be orthogonal over
$\binom{|{\mathrm{supp}}(v)|}{k - 1} \varepsilon |{\mathrm{supp}}(v)|$
will be orthogonal over
![]() $\mathbb{Z}/q\mathbb{Z}$
to
$\mathbb{Z}/q\mathbb{Z}$
to
![]() $v$
. To construct a vector
$v$
. To construct a vector
![]() $w$
in
$w$
in
![]() $V_{k, n}^v$
that’s orthogonal to
$V_{k, n}^v$
that’s orthogonal to
![]() $v$
we first pick the first
$v$
we first pick the first
![]() $k - 1$
positions in
$k - 1$
positions in
![]() ${\mathrm{supp}}(v)$
to be nonzero in
${\mathrm{supp}}(v)$
to be nonzero in
![]() $w$
. Clearly there are at most
$w$
. Clearly there are at most
![]() $\binom{|{\mathrm{supp}}(v)|}{k - 1}$
ways to do this. If
$\binom{|{\mathrm{supp}}(v)|}{k - 1}$
ways to do this. If
![]() $w'$
denotes this vector (in
$w'$
denotes this vector (in
![]() $V_{k -1, n}^v$
) then if
$V_{k -1, n}^v$
) then if
![]() $w' \cdot v = 0$
then there is no way to select the last position of the nonzero entry in
$w' \cdot v = 0$
then there is no way to select the last position of the nonzero entry in
![]() $w$
so that
$w$
so that
![]() ${\mathrm{supp}}(w) \subseteq{\mathrm{supp}}(v)$
and
${\mathrm{supp}}(w) \subseteq{\mathrm{supp}}(v)$
and
![]() $w \cdot v = 0$
. On the other hand if
$w \cdot v = 0$
. On the other hand if
![]() $w' \cdot v \neq 0$
then in order for
$w' \cdot v \neq 0$
then in order for
![]() $w \cdot v$
to be zero, and the last entry of
$w \cdot v$
to be zero, and the last entry of
![]() $w$
must fall into a position where
$w$
must fall into a position where
![]() $v$
is the unique non-zero element of
$v$
is the unique non-zero element of
![]() $\mathbb{Z}/q\mathbb{Z}$
equal to
$\mathbb{Z}/q\mathbb{Z}$
equal to
![]() $-w' \cdot v$
. By the
$-w' \cdot v$
. By the
![]() $\varepsilon$
-balanced condition, there are at most
$\varepsilon$
-balanced condition, there are at most
![]() $\varepsilon |{\mathrm{supp}}(v)|$
choices for this position. Thus
$\varepsilon |{\mathrm{supp}}(v)|$
choices for this position. Thus
![]() $V_{k, n}^v$
has
$V_{k, n}^v$
has
![]() $\binom{|{\mathrm{supp}}(v)|}{k}$
vectors and at most
$\binom{|{\mathrm{supp}}(v)|}{k}$
vectors and at most
![]() $\binom{|{\mathrm{supp}}(v)|}{k - 1} \varepsilon |{\mathrm{supp}}(v)|$
of them are orthogonal to
$\binom{|{\mathrm{supp}}(v)|}{k - 1} \varepsilon |{\mathrm{supp}}(v)|$
of them are orthogonal to
![]() $v$
.
$v$
.
Suppose on the other hand, that
![]() $v$
is not
$v$
is not
![]() $\varepsilon$
-balanced. Then there is some subset
$\varepsilon$
-balanced. Then there is some subset
![]() $S$
of
$S$
of
![]() ${\mathrm{supp}}(v)$
with
${\mathrm{supp}}(v)$
with
![]() $|S| \geq \varepsilon |{\mathrm{supp}}(v)|$
so that
$|S| \geq \varepsilon |{\mathrm{supp}}(v)|$
so that
![]() $v$
restricted to
$v$
restricted to
![]() $S$
is a constant, nonzero function in
$S$
is a constant, nonzero function in
![]() $\mathbb{Z}/q\mathbb{Z}$
. Then any vector in
$\mathbb{Z}/q\mathbb{Z}$
. Then any vector in
![]() $V_{k, n}$
with support contained in
$V_{k, n}$
with support contained in
![]() $S$
cannot be orthogonal to
$S$
cannot be orthogonal to
![]() $v$
as the dot product of
$v$
as the dot product of
![]() $v$
with such a vector is simply
$v$
with such a vector is simply
![]() $x - x + x - x \cdots + x = x$
. Thus, there are at least
$x - x + x - x \cdots + x = x$
. Thus, there are at least
vectors in
![]() $V_{k, n}$
that are not orthogonal to
$V_{k, n}$
that are not orthogonal to
![]() $v$
when
$v$
when
![]() $v$
is not
$v$
is not
![]() $\varepsilon$
balanced. Thus, we have the claim with
$\varepsilon$
balanced. Thus, we have the claim with
 \begin{equation*}\gamma = \min\!\left \{\frac {1}{k^k} - \frac {\varepsilon }{(k - 1)!}, \frac {\varepsilon ^k}{k^k} \right \}.\end{equation*}
\begin{equation*}\gamma = \min\!\left \{\frac {1}{k^k} - \frac {\varepsilon }{(k - 1)!}, \frac {\varepsilon ^k}{k^k} \right \}.\end{equation*}
Now we prove Lemma 6.
Proof of Lemma
6
. Consider the stochastic process to build
![]() $M^T$
one row at a time. Let
$M^T$
one row at a time. Let
![]() $M^T_i$
denote the
$M^T_i$
denote the
![]() $i \times n$
matrix at step
$i \times n$
matrix at step
![]() $i$
and let
$i$
and let
![]() $Z_i$
be the random variable
$Z_i$
be the random variable
![]() $\dim\!(\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T_i))$
with the convention that
$\dim\!(\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T_i))$
with the convention that
![]() $Z_0 = n$
. If
$Z_0 = n$
. If
![]() $M^T_i$
has a vector of support size at least
$M^T_i$
has a vector of support size at least
![]() $\delta n$
in its kernel over
$\delta n$
in its kernel over
![]() $\mathbb{Z}/q\mathbb{Z}$
then the probability that
$\mathbb{Z}/q\mathbb{Z}$
then the probability that
![]() $K_{i + 1} \lt K_i$
is at least
$K_{i + 1} \lt K_i$
is at least
where
![]() $\gamma$
is as in Lemma 13. Thus the probability that
$\gamma$
is as in Lemma 13. Thus the probability that
![]() $M^T_{cn}$
for
$M^T_{cn}$
for
![]() $c$
a large constant has a kernel element over
$c$
a large constant has a kernel element over
![]() $\mathbb{Z}/q\mathbb{Z}$
of support size at least
$\mathbb{Z}/q\mathbb{Z}$
of support size at least
![]() $\delta n$
is at most the probability that a binomial random variable with
$\delta n$
is at most the probability that a binomial random variable with
![]() $cn$
trials and success probability
$cn$
trials and success probability
![]() $k! \delta ^k \gamma$
has at most
$k! \delta ^k \gamma$
has at most
![]() $n$
successes. By Chernoff’s bound this is at most
$n$
successes. By Chernoff’s bound this is at most
![]() $\exp\!(\!-\!Cn)$
where
$\exp\!(\!-\!Cn)$
where
![]() $C$
can be made an arbitrarily large constant by setting
$C$
can be made an arbitrarily large constant by setting
![]() $c$
large enough.
$c$
large enough.
Now we turn our attention to the even case. Fortunately the relevant definition we need is the
![]() $\varepsilon$
-balanced definition we have already introduced. The analogue of Lemma 6 is the following:
$\varepsilon$
-balanced definition we have already introduced. The analogue of Lemma 6 is the following:
Lemma 15.
For any
![]() $k \geq 4$
even,
$k \geq 4$
even,
![]() $\delta \gt 0$
, and
$\delta \gt 0$
, and
![]() $0 \lt \varepsilon \lt \frac{(k -1)!}{k^k}$
and
$0 \lt \varepsilon \lt \frac{(k -1)!}{k^k}$
and
![]() $c = c(k, \delta, \varepsilon )$
sufficiently large there exists
$c = c(k, \delta, \varepsilon )$
sufficiently large there exists
![]() $C = C(c) \gt \log\!(k)$
so that for any prime
$C = C(c) \gt \log\!(k)$
so that for any prime
![]() $q$
the probability that
$q$
the probability that
![]() $\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
for
$\ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
for
![]() $M = M(\mathcal{H})$
,
$M = M(\mathcal{H})$
,
![]() $\mathcal{H} \sim \mathcal{H}_k(n, cn)$
contains an
$\mathcal{H} \sim \mathcal{H}_k(n, cn)$
contains an
![]() $\varepsilon$
-balanced vector of support size at least
$\varepsilon$
-balanced vector of support size at least
![]() $\delta n$
is at most
$\delta n$
is at most
![]() $e^{-Cn}$
.
$e^{-Cn}$
.
The proof of this proceeds from the following lemma exactly as the proof of Lemma 6.
Lemma 16.
For
![]() $k \geq 4$
even and
$k \geq 4$
even and
![]() $0 \lt \varepsilon \lt \frac{(k - 1)!}{k^k}$
there exists
$0 \lt \varepsilon \lt \frac{(k - 1)!}{k^k}$
there exists
![]() $\gamma = \gamma (k, \varepsilon )$
so that for any prime
$\gamma = \gamma (k, \varepsilon )$
so that for any prime
![]() $q$
and every
$q$
and every
![]() $\varepsilon$
-balanced vector
$\varepsilon$
-balanced vector
![]() $v \in (\mathbb{Z}/q\mathbb{Z})^n$
,
$v \in (\mathbb{Z}/q\mathbb{Z})^n$
,
![]() $|B_q(v)| \geq \gamma |{\mathrm{supp}}(v)|^k$
.
$|B_q(v)| \geq \gamma |{\mathrm{supp}}(v)|^k$
.
The proof of Lemma 16 is exactly the
![]() $\varepsilon$
-balanced case of the proof of Lemma 13. Now we are ready to prove Theorem 2 in the case that
$\varepsilon$
-balanced case of the proof of Lemma 13. Now we are ready to prove Theorem 2 in the case that
![]() $k$
is even.
$k$
is even.
Proof of Theorem
2 for even k. As in the odd
![]() $k$
case it suffices to show that with high probability there are no
$k$
case it suffices to show that with high probability there are no
![]() $v$
,
$v$
,
![]() $w$
, and
$w$
, and
![]() $q$
so that
$q$
so that
![]() $M^Tv = qw$
,
$M^Tv = qw$
,
![]() $w \notin \text{Im}(M^T)$
and
$w \notin \text{Im}(M^T)$
and
![]() $v \notin (q\mathbb{Z})^n$
. Fix a positive
$v \notin (q\mathbb{Z})^n$
. Fix a positive
![]() $\varepsilon \lt (k - 1)!/k^k$
and take
$\varepsilon \lt (k - 1)!/k^k$
and take
![]() $\delta = (1 + \varepsilon )^{-1}$
. By Lemma 10 the probability that
$\delta = (1 + \varepsilon )^{-1}$
. By Lemma 10 the probability that
![]() $M^T$
has a torsion cocycle of size at most
$M^T$
has a torsion cocycle of size at most
![]() $\delta n$
is
$\delta n$
is
![]() $o(1)$
. If
$o(1)$
. If
![]() $M^Tv = qw$
with
$M^Tv = qw$
with
![]() $S \;:\!=\;{\mathrm{supp}}(v)$
of size at most
$S \;:\!=\;{\mathrm{supp}}(v)$
of size at most
![]() $\delta n$
then we use the fact that with high probability
$\delta n$
then we use the fact that with high probability
![]() ${\mathrm{coker}}((M^T)_S)$
is torsion-free to conclude that
${\mathrm{coker}}((M^T)_S)$
is torsion-free to conclude that
![]() $w \in \text{Im}(M^T)$
.
$w \in \text{Im}(M^T)$
.
For vectors of large support, by a similar union bound to the odd
![]() $k$
case we can use Lemmas 15 and 7 to rule out
$k$
case we can use Lemmas 15 and 7 to rule out
![]() $\varepsilon$
-balanced vector
$\varepsilon$
-balanced vector
![]() $v \in \mathbb{Z}/q\mathbb{Z}$
with
$v \in \mathbb{Z}/q\mathbb{Z}$
with
![]() $|{\mathrm{supp}}(v)| \geq \delta n$
and
$|{\mathrm{supp}}(v)| \geq \delta n$
and
![]() $v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
. The only case that’s different is if
$v \in \ker _{\mathbb{Z}/q\mathbb{Z}}(M^T)$
. The only case that’s different is if
![]() $v$
is not
$v$
is not
![]() $\varepsilon$
-balanced but still has large support. If
$\varepsilon$
-balanced but still has large support. If
![]() $v$
is not
$v$
is not
![]() $\varepsilon$
-balanced then some
$\varepsilon$
-balanced then some
![]() $x \in \mathbb{Z}/q\mathbb{Z} \setminus \{0\}$
appears more than
$x \in \mathbb{Z}/q\mathbb{Z} \setminus \{0\}$
appears more than
![]() $\varepsilon \delta n$
times in
$\varepsilon \delta n$
times in
![]() $v$
. In this case then
$v$
. In this case then
![]() $x\textbf{1} - v$
satisfies
$x\textbf{1} - v$
satisfies
![]() $|{\mathrm{supp}}(x\textbf{1} - v)| \leq n - \varepsilon \delta n = \delta n$
, and
$|{\mathrm{supp}}(x\textbf{1} - v)| \leq n - \varepsilon \delta n = \delta n$
, and
![]() $M^T(x \textbf{1} - v) = -qw$
, but then
$M^T(x \textbf{1} - v) = -qw$
, but then
![]() $S ={\mathrm{supp}}(x \textbf{1} - v)$
has size at most
$S ={\mathrm{supp}}(x \textbf{1} - v)$
has size at most
![]() $\delta n$
so we appeal again to the fact that
$\delta n$
so we appeal again to the fact that
![]() ${\mathrm{coker}}((M^T)_S)$
has no
${\mathrm{coker}}((M^T)_S)$
has no
![]() $q$
-torsion to conclude that
$q$
-torsion to conclude that
![]() $w \in \text{Im}(M^T)$
.
$w \in \text{Im}(M^T)$
.
5. Proof of Theorem 4
For the proof of Theorem 4, we use Theorem 2 as well as a theorem of Cooper, Frieze, and Pegden [Reference Cooper, Frieze and Pegden6]. In [Reference Cooper, Frieze and Pegden6], the authors consider the same model that we consider except that the matrices are taken over
![]() $\mathbb{Z}/2\mathbb{Z}$
rather than over
$\mathbb{Z}/2\mathbb{Z}$
rather than over
![]() $\mathbb{Z}$
. Theorem 1.3 from [Reference Cooper, Frieze and Pegden6] and the usual coupling argument between
$\mathbb{Z}$
. Theorem 1.3 from [Reference Cooper, Frieze and Pegden6] and the usual coupling argument between
![]() $\mathcal{H}_k(n, p)$
and
$\mathcal{H}_k(n, p)$
and
![]() $\mathcal{H}_k(n, m)$
immediately give the following.
$\mathcal{H}_k(n, m)$
immediately give the following.
Theorem 17. (Corollary to Theorem 1.3 of [Reference Cooper, Frieze and Pegden6]). Let
![]() $n^* \;:\!=\; n$
, if
$n^* \;:\!=\; n$
, if
![]() $k$
is odd, and
$k$
is odd, and
![]() $n^* \;:\!=\; n - 1$
, if
$n^* \;:\!=\; n - 1$
, if
![]() $k$
is even. For
$k$
is even. For
![]() $p = \frac{c \log n}{n^{k - 1}}$
the following hold for
$p = \frac{c \log n}{n^{k - 1}}$
the following hold for
![]() $\mathcal{H}_k(n, p)$
.
$\mathcal{H}_k(n, p)$
.
-
• If
 $c \lt k!$
then with high probability
$c \lt k!$
then with high probability
 ${\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M(\mathcal{H}))$
is smaller than
${\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M(\mathcal{H}))$
is smaller than
 $n^*$
.
$n^*$
. -
• If
 $c \gt k!$
then with high probability
$c \gt k!$
then with high probability
 ${\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M(\mathcal{H}))$
is equal to
${\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M(\mathcal{H}))$
is equal to
 $n^*$
.
$n^*$
.
We can now give a short proof of Theorem 4.
Proof of Theorem
4
. For any matrix
![]() $m \times n$
matrix
$m \times n$
matrix
![]() $M$
the cokernel of
$M$
the cokernel of
![]() $M$
can be read off of the elementary divisors of
$M$
can be read off of the elementary divisors of
![]() $M$
, so in particular the free part of
$M$
, so in particular the free part of
![]() ${\mathrm{coker}}(M)$
is
${\mathrm{coker}}(M)$
is
![]() $\mathbb{Z}^{n -{\mathrm{rank}}_{\mathbb{Q}}(M)}$
. Moreover the inequality
$\mathbb{Z}^{n -{\mathrm{rank}}_{\mathbb{Q}}(M)}$
. Moreover the inequality
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M) \geq{\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M)$
for
${\mathrm{rank}}_{\mathbb{Q}}(M) \geq{\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M)$
for
![]() $M$
an integer matrix always holds since
$M$
an integer matrix always holds since
![]() $Mv =0$
over
$Mv =0$
over
![]() $\mathbb{Q}$
implies that
$\mathbb{Q}$
implies that
![]() $Mv = 0$
over
$Mv = 0$
over
![]() $\mathbb{Z}/2\mathbb{Z}$
. For
$\mathbb{Z}/2\mathbb{Z}$
. For
![]() $c \lt k!$
by Theorem 17, with high probability the free part of
$c \lt k!$
by Theorem 17, with high probability the free part of
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
has rank larger than
${\mathrm{coker}}(M(\mathcal{H}))$
has rank larger than
![]() $n - n^*$
. Thus we have the first part of Theorem 4.
$n - n^*$
. Thus we have the first part of Theorem 4.
For
![]() $c \gt k!$
, we know that
$c \gt k!$
, we know that
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M(\mathcal{H})) \geq{\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M(\mathcal{H})) = n^*$
asymptotically almost surely, and trivially
${\mathrm{rank}}_{\mathbb{Q}}(M(\mathcal{H})) \geq{\mathrm{rank}}_{\mathbb{Z}/2\mathbb{Z}}(M(\mathcal{H})) = n^*$
asymptotically almost surely, and trivially
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M(\mathcal{H})) \leq n^*$
. Thus
${\mathrm{rank}}_{\mathbb{Q}}(M(\mathcal{H})) \leq n^*$
. Thus
![]() ${\mathrm{rank}}_{\mathbb{Q}}(M(\mathcal{H})) = n^*$
in this regime. Thus for
${\mathrm{rank}}_{\mathbb{Q}}(M(\mathcal{H})) = n^*$
in this regime. Thus for
![]() $k$
odd, with high probability
$k$
odd, with high probability
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
is finite, and for
${\mathrm{coker}}(M(\mathcal{H}))$
is finite, and for
![]() $k$
even, with high probability
$k$
even, with high probability
![]() ${\mathrm{coker}}(M(\mathcal{H})) = \mathbb{Z} \oplus A$
for some finite abelian group
${\mathrm{coker}}(M(\mathcal{H})) = \mathbb{Z} \oplus A$
for some finite abelian group
![]() $A$
. However we know by Theorem 2 that
$A$
. However we know by Theorem 2 that
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
is torsion-free, so we conclude in the odd
${\mathrm{coker}}(M(\mathcal{H}))$
is torsion-free, so we conclude in the odd
![]() $k$
case we are left with the trivial group and in the even
$k$
case we are left with the trivial group and in the even
![]() $k$
case we are left with
$k$
case we are left with
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
6. Concluding remarks
The main result here was motivated by the conjecture of Łuczak and Peled about random simplicial complexes described earlier. Based on Theorem 2 it would seem plausible that an adaptation of the methods here could be used to show that
![]() $p = \omega (1/n)$
implies that
$p = \omega (1/n)$
implies that
![]() $H_{d - 1}(Y)$
for
$H_{d - 1}(Y)$
for
![]() $Y \sim Y_d(n, p)$
is torsion-free with high probability.
$Y \sim Y_d(n, p)$
is torsion-free with high probability.
In another direction, it would be interesting to extend the model for
![]() $M(\mathcal{H})$
here to allow for the nonzero entries to come from a sequence other than
$M(\mathcal{H})$
here to allow for the nonzero entries to come from a sequence other than
![]() $1, -1, 1, -1, \ldots$
. For example, if we instead defined
$1, -1, 1, -1, \ldots$
. For example, if we instead defined
![]() $M(\mathcal{H})$
by having the nonzero entries all be equal to 1, then clearly
$M(\mathcal{H})$
by having the nonzero entries all be equal to 1, then clearly
![]() $\textbf{1}$
is an element of the kernel of
$\textbf{1}$
is an element of the kernel of
![]() $M^T$
for primes that divide
$M^T$
for primes that divide
![]() $k$
, but not over
$k$
, but not over
![]() $\mathbb{Q}$
, and so there would always be
$\mathbb{Q}$
, and so there would always be
![]() $k$
-torsion even when
$k$
-torsion even when
![]() $p = 1$
. Nonetheless, it seems likely that in this version of the model one could show that for
$p = 1$
. Nonetheless, it seems likely that in this version of the model one could show that for
![]() $p = \omega (1/n^{k - 1})$
with high probability there is no torsion other than the torsion which exists in
$p = \omega (1/n^{k - 1})$
with high probability there is no torsion other than the torsion which exists in
![]() ${\mathrm{coker}}(M(\mathcal{H}))$
for
${\mathrm{coker}}(M(\mathcal{H}))$
for
![]() $\mathcal{H}$
the complete
$\mathcal{H}$
the complete
![]() $k$
-uniform hypergraph on
$k$
-uniform hypergraph on
![]() $n$
vertices, which would be
$n$
vertices, which would be
![]() $\mathbb{Z}/k\mathbb{Z}$
.
$\mathbb{Z}/k\mathbb{Z}$
.
Acknowledgments
The author thanks Elliot Paquette for helpful discussions at the beginning of the research for this article and for comments on an earlier draft. The author also thanks the anonymous referees for helpful remarks. Some portions of this work were funded by the National Science Foundation grants NSF-DMS #1547357 and #60041693