Bipartite-ness under smooth conditions

Abstract

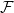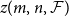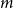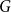Given a family $\mathcal{F}$ of bipartite graphs, the Zarankiewicz number $z(m,n,\mathcal{F})$ is the maximum number of edges in an $m$ by $n$ bipartite graph $G$ that does not contain any member of 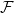$\mathcal{F}$ as a subgraph (such 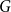$G$ is called 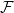$\mathcal{F}$-free). For 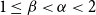$1\leq \beta \lt \alpha \lt 2$, a family 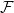$\mathcal{F}$ of bipartite graphs is 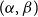$(\alpha,\beta )$-smooth if for some 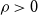$\rho \gt 0$ and every 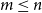$m\leq n$, 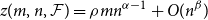$z(m,n,\mathcal{F})=\rho m n^{\alpha -1}+O(n^\beta )$. Motivated by their work on a conjecture of Erdős and Simonovits on compactness and a classic result of Andrásfai, Erdős and Sós, Allen, Keevash, Sudakov and Verstraëte proved that for any 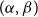$(\alpha,\beta )$-smooth family 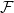$\mathcal{F}$, there exists 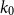$k_0$ such that for all odd 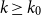$k\geq k_0$ and sufficiently large $n$, any $n$-vertex 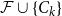$\mathcal{F}\cup \{C_k\}$-free graph with minimum degree at least 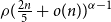$\rho (\frac{2n}{5}+o(n))^{\alpha -1}$ is bipartite. In this paper, we strengthen their result by showing that for every real 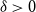$\delta \gt 0$, there exists 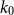$k_0$ such that for all odd 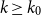$k\geq k_0$ and sufficiently large $n$, any $n$-vertex 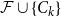$\mathcal{F}\cup \{C_k\}$-free graph with minimum degree at least 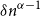$\delta n^{\alpha -1}$ is bipartite. Furthermore, our result holds under a more relaxed notion of smoothness, which include the families 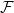$\mathcal{F}$ consisting of the single graph 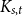$K_{s,t}$ when 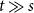$t\gg s$. We also prove an analogous result for 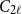$C_{2\ell }$-free graphs for every 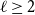$\ell \geq 2$, which complements a result of Keevash, Sudakov and Verstraëte.