Hostname: page-component-7dd5485656-bvgqh Total loading time: 0 Render date: 2025-10-30T16:16:33.671Z Has data issue: false hasContentIssue false
  • English
  • Français

Irregular subgraphs

Part of: Graph theory

Published online by Cambridge University Press:  23 September 2022

Noga Alon  and
Fan Wei
Noga Alon
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA Schools of Mathematics and Computer Science, Tel Aviv University, Tel Aviv 69978, Israel
Fan Wei*
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ 08544, USA
*
*Corresponding author. Email: fanw@princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We suggest two related conjectures dealing with the existence of spanning irregular subgraphs of graphs. The first asserts that any 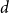$d$-regular graph on $n$ vertices contains a spanning subgraph in which the number of vertices of each degree between 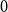$0$ and 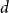$d$ deviates from 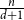$\frac{n}{d+1}$ by at most 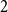$2$. The second is that every graph on $n$ vertices with minimum degree 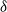$\delta$ contains a spanning subgraph in which the number of vertices of each degree does not exceed 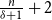$\frac{n}{\delta +1}+2$. Both conjectures remain open, but we prove several asymptotic relaxations for graphs with a large number of vertices $n$. In particular we show that if 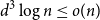$d^3 \log n \leq o(n)$ then every 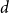$d$-regular graph with $n$ vertices contains a spanning subgraph in which the number of vertices of each degree between 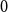$0$ and 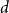$d$ is 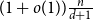$(1+o(1))\frac{n}{d+1}$. We also prove that any graph with $n$ vertices and minimum degree 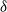$\delta$ contains a spanning subgraph in which no degree is repeated more than 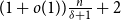$(1+o(1))\frac{n}{\delta +1}+2$ times.

Keywords

irregular subgraphrepeated degrees

MSC classification

Primary: 05C35: Extremal problems
Secondary: 05C07: Vertex degrees

Information

Type
Paper
Information
Combinatorics, Probability and Computing , Volume 32 , Issue 2 , March 2023 , pp. 269 - 283
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

†

Research supported in part by NSF grant DMS-2154082 and BSF grant 2018267.

‡

Research supported by NSF Award DMS-1953958.

References

Addario-Berry, L., Dalal, K. and Reed, B. A. (2005) Degree constrained subgraphs. In Proceedings of GRACO2005, Vol. 19 of Electronic Notes in Discrete Mathematics, Elsevier, pp. 257–263.CrossRefGoogle Scholar
Axenovich, M. and Füredi, Z. (2001) Embedding of graphs in two-irregular graphs. J. Graph Theory 36(2) 75–83.3.0.CO;2-E>CrossRefGoogle Scholar
Alon, N. and Spencer, J. H. (2016) The Probabilistic Method, fourth edition, Wiley, xiv+375pp.Google Scholar
Beck, J. and Fiala, T. (1981) Integer-making theorems. Disc. Appl. Math. 3(1) 1–8.CrossRefGoogle Scholar
Chartrand, G., Jacobson, M. S., Lehel, J., Oellermann, O. R., Ruiz, S. and Saba, F. (1986) Irregular networks. In Proceedings of 250th Anniversary Conference on Graph Theory, Fort Wayne, Indiana.Google Scholar
Cuckler, B. and Lazebnik, F. (2008) Irregularity strength of dense graphs. J. Graph Theory 58(4) 299–313.CrossRefGoogle Scholar
Faudree, R. J. and Lehel, J. (1987) Bound on the Irregularity Strength of Regular Graphs, Vol. 52 of Colloq. Math. Soc. Janos Bolyai, North Holland, pp. 247–256.Google Scholar
Frieze, A., Gould, R. J., Karoński, M. and Pfender, F. (2002) On graph irregularity strength. J. Graph Theory 41(2) 120–137.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of Erdős. In Combinatorial Theory and its Applications, Vol. II(P. Erdős, A. Rényi and V. T. Sós, eds), Vol. 4 of Colloq. Math. Soc. J. Bolyai, North Holland, pp. 601–623.Google Scholar
Kalkowski, M., Karoński, M. and Pfender, F. (2011) A new upper bound for the irregularity strength of graphs. SIAM J. Discrete Math. 25(3) 1319–1321.CrossRefGoogle Scholar
Lehel, J. (1991) Facts and quests on degree irregular assignments. In Graph Theory, Combinatorics and Applications, Wiley, pp. 765–782.Google Scholar
Majerski, P. and Przybyło, J. (2014) On the irregularity strength of dense graphs. SIAM J. Discrete Math. 28(1) 197–205.CrossRefGoogle Scholar
Przybyło, J. (2008) Irregularity strength of regular graphs. Electron J. Combin. 15(1) 10. Research Paper 82.CrossRefGoogle Scholar
Przybyło, J. (2008/2009) Linear bound on the irregularity strength and the total vertex irregularity strength of graphs. SIAM J. Discrete Math. 23 511–516.CrossRefGoogle Scholar
Przybyło, J. (2022) Asymptotic confirmation of the Faudree-Lehel conjecture on irregularity strength for all but extreme degrees. J. Graph Theory 100(1) 189–204.CrossRefGoogle Scholar
Przybyło, J. and Wei, F. (2021) On the asymptotic confirmation of the Faudree-Lehel Conjecture for general graphs, arXiv:2109.04317.Google Scholar
Schrijver, A. (2003) Combinatorial Optimization, Polyhedra and Efficiency, Vol. A. Paths, Flows, Matchings,Vol. 24 of Algorithms and Combinatorics, Springer, xxxviii+647pp.Google Scholar