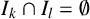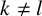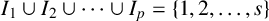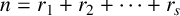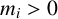Search

In this article, we clarify the relation between the squeezing function and the Fridman invariant corresponding to a general domain $\Omega $ (not necessarily convex), where $\Omega $ is defined by

$$ \begin{align*}\Omega = \bigg\lbrace z \in \mathbb{C}^{r_{1}}\times\mathbb{C}^{r_{2}}\times\cdots\times\mathbb{C}^{r_{s}} : \sum\limits_{i\in I_{k}} ||z_{i}||^{m_{i}} < 1, 1\leq k \leq p \bigg\rbrace,\end{align*} $$

with 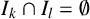$I_{k}\cap I_{l} = \emptyset $ if 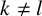$k\neq l$, 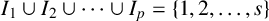$I_{1}\cup I_{2} \cup \cdots \cup I_{p} = \lbrace 1, 2, \ldots , s\rbrace $, 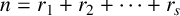$n = r_{1} + r_{2} + \cdots + r_{s}$ and 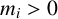$m_{i}> 0$ for all i. Furthermore, we give an example of a domain whose squeezing function corresponding to $\Omega $ is not plurisubharmonic.

Search Results

Refine search

Refine search

Actions for selected content:

2 results

ON THE GENERALISED SQUEEZING FUNCTION

A DOMAIN WITH NONPLURISUBHARMONIC d-BALANCED SQUEEZING FUNCTION

Search Results

Refine search

Refine search

Actions for selected content:

Save Search

2 results

ON THE GENERALISED SQUEEZING FUNCTION

A DOMAIN WITH NONPLURISUBHARMONIC d-BALANCED SQUEEZING FUNCTION