Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T17:15:43.640Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic properties of random Voronoi cells with arbitrary underlying density

Part of: Geometric probability and stochastic geometry Stochastic processes

Published online by Cambridge University Press:  15 July 2020

Isaac Gibbs  and
Linan Chen Open the ORCID record for Linan Chen [Opens in a new window]
Isaac Gibbs*
Affiliation:
Stanford University
Linan Chen*
Affiliation:
McGill University
*
*Postal address: Department of Statistics, Stanford University, 390 Jane Stanford Way, Stanford, CA 94305, USA. Email address: igibbs@stanford.edu
**Postal address: Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montreal, Quebec, H3A 0B9, Canada. Email address: linan.chen@mcgill.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Voronoi diagram generated by n independent and identically distributed 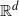$\mathbb{R}^{d}$ -valued random variables with an arbitrary underlying probability density function f on 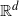$\mathbb{R}^{d}$ , and analyze the asymptotic behaviors of certain geometric properties, such as the measure, of the Voronoi cells as n tends to infinity. We adapt the methods used by Devroye et al. (2017) to conduct a study of the asymptotic properties of two types of Voronoi cells: (1) Voronoi cells that have a fixed nucleus; (2) Voronoi cells that contain a fixed point. We show that the geometric properties of both types of cells resemble those in the case when the Voronoi diagram is generated by a homogeneous Poisson point process. Additionally, for the second type of Voronoi cells, we determine the limiting distribution, which is universal in all choices of f, of the re-scaled measure of the cells.

Keywords

Point process with arbitrary densitygeometry of random Voronoi diagramconvergence in distribution

MSC classification

Primary: 60G55: Point processes
Secondary: 60D05: Geometric probability and stochastic geometry
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 2 , June 2020 , pp. 655 - 680
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrews, J. G., Baccelli, F. and Ganti, R. K. (2008). A tractable approach to coverage and rate in cellular networks. IEEE Trans. Commun. 59, 3122–3134.10.1109/TCOMM.2011.100411.100541CrossRefGoogle Scholar
Biau, G. and Devroye, L. (2015). Lectures on the Nearest Neighbour Method. Springer, Cham.10.1007/978-3-319-25388-6CrossRefGoogle Scholar
Billingsley, P. (1986). Probability and Measure, 2nd edn. John Wiley, New York.Google Scholar
Brakke, K. A. (2005). Statistics of random plane Voronoi tessellations. Unpublished manuscript.Google Scholar
Brakke, K. A. (2005). Statistics of three dimensional random Voronoi tessellations. Unpublished manuscript.Google Scholar
Chernoff, H. (1952). A measure of asymptotic efficiency for tests of a hypothesis based on the sum of observations. 23, 493–507.10.1214/aoms/1177729330CrossRefGoogle Scholar
Devroye, L., Györfi, L., Lugosi, G. and Walk, H. (2017). On the measure of Voronoi cells. J. Appl. Prob. 54, 394–408.10.1017/jpr.2017.7CrossRefGoogle Scholar
Devroye, L., Györfi, L., Lugosi, G., and Walk, H. (2018). A nearest neighbour estimate of the residual variance. Electron. J. Statist. 12, 1752–1778.10.1214/18-EJS1438CrossRefGoogle Scholar
Devroye, L. and Lugosi, G. (2001). Combinatorial Methods in Density Estimation, 1st edn. Springer, New York.10.1007/978-1-4613-0125-7CrossRefGoogle Scholar
Gilbert, E. N. (1962). Random subdivisions of space into crystals. Ann. Math. Statist. 33, 958–972.10.1214/aoms/1177704464CrossRefGoogle Scholar
Hayen, A. and Quine, M. P. (2002). Areas of components of a Voronoi polygon in a homogeneous Poisson process in the plane. Adv. Appl. Prob. 34, 281–291.10.1239/aap/1025131218CrossRefGoogle Scholar
Heinrich, L., Körner, R., Mehlhorn, N. and Muche, L. (1998). Numerical and analytical computation of some second-order characteristics of spatial Poisson–Voronoi tessellations. Statistics 31, 235–259.10.1080/02331889808802638CrossRefGoogle Scholar
Heinrich, L. and Muche, L. (2010). Second-order properties of the point process of nodes in a stationary Voronoi tessellation. Math. Nachr. 281, 350–375. (Erratum: 283 (2010), 1674–1676.)CrossRefGoogle Scholar
Meijering, J. (1953). Interface area, edge length, and number of vertices in crystal aggregation with random nucleation. Philips Res. Rep. 8, 270–290.Google Scholar
Møller, J. (1994). Lectures on Random Voronoi Tessellations, 1st edn. Springer, New York.CrossRefGoogle Scholar
Neyrinck, M. C. (2008). ZOBOV: a parameter-free void-finding algorithm. Mon. Not. R. Astron. Soc. 386, 2101–2109.10.1111/j.1365-2966.2008.13180.xCrossRefGoogle Scholar
Okabe, A., Boots, B., Sugihara, K. and Chiu, S. N. (2000). Spatial Tessellations: Concepts and Applications of Voronoi Diagrams, 2nd edn. John Wiley, New York.10.1002/9780470317013CrossRefGoogle Scholar
Pinto, P. C., Barros, J. and Win, M. Z. (2012). Secure communications in stochastic wireless networks—Part I: connectivity. IEEE Trans. Inf. Forens. Sec. 7, 125–138.10.1109/TIFS.2011.2165946CrossRefGoogle Scholar
Rosenblatt, M. (1956). Remarks on some nonparametric estimates of a density. 27, 832–837.10.1214/aoms/1177728190CrossRefGoogle Scholar
Scott, D. W. (2015). Multivariate Density Estimation: Theory, Practice, and Visualization, 2nd edn. John Wiley, New York.10.1002/9781118575574CrossRefGoogle Scholar
Vittorietti, M., Jongbloed, G., Kok, P. J. J. and Sietsma, J. (2017). Accurate approximation of the distributions of the 3D Poisson–Voronoi typical cell geometrical features. Preprint.Google Scholar