Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T21:47:29.426Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of the conditional stationary distribution in Markov chains via systems of linear inequalities

Part of: Markov processes Special processes

Published online by Cambridge University Press:  03 December 2020

Masatoshi Kimura  and
Tetsuya Takine
Masatoshi Kimura*
Affiliation:
Osaka University
Tetsuya Takine*
Affiliation:
Osaka University
*
*Postal address: Department of Information and Communications Technology, Graduate School of Engineering, Osaka University, Suita 565-0871, Japan.
*Postal address: Department of Information and Communications Technology, Graduate School of Engineering, Osaka University, Suita 565-0871, Japan.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper considers ergodic, continuous-time Markov chains 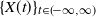$\{X(t)\}_{t \in (\!-\infty,\infty)}$ on 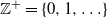$\mathbb{Z}^+=\{0,1,\ldots\}$ . For an arbitrarily fixed 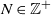$N \in \mathbb{Z}^+$ , we study the conditional stationary distribution 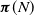$\boldsymbol{\pi}(N)$ given the Markov chain being in 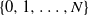$\{0,1,\ldots,N\}$ . We first characterize 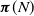$\boldsymbol{\pi}(N)$ via systems of linear inequalities and identify simplices that contain 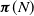$\boldsymbol{\pi}(N)$ , by examining the 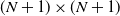$(N+1) \times (N+1)$ northwest corner block of the infinitesimal generator 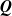$\textbf{\textit{Q}}$ and the subset of the first 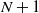$N+1$ states whose members are directly reachable from at least one state in 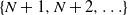$\{N+1,N+2,\ldots\}$ . These results are closely related to the augmented truncation approximation (ATA), and we provide some practical implications for the ATA. Next we consider an extension of the above results, using the 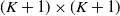$(K+1) \times (K+1)$ ( 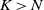$K > N$ ) northwest corner block of 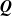$\textbf{\textit{Q}}$ and the subset of the first 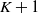$K+1$ states whose members are directly reachable from at least one state in 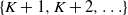$\{K+1,K+2,\ldots\}$ . Furthermore, we introduce new state transition structures called (K, N)-skip-free sets, using which we obtain the minimum convex polytope that contains 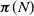$\boldsymbol{\pi}(N)$ .

Keywords

Markov chainscountably infinite state spaceconditional stationary distributionlinear inequalitiesconvex polytopesaugmented truncation approximation

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces
Secondary: 60K25: Queueing theory
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 4 , December 2020 , pp. 1249 - 1283
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bright, L. and Taylor, P. G. (1995). Calculating the equilibrium distribution in level dependent quasi-birth-and-death processes. Stoch. Models 11, 497–525.CrossRefGoogle Scholar
Gibson, D. and Seneta, E. (1987). Augmented truncations of infinite stochastic matrices. J. Appl. Prob. 24, 600–608.CrossRefGoogle Scholar
Grunbaum, B. (2003). Convex Polytopes, 2nd edn. Springer, New York, NY.CrossRefGoogle Scholar
Hart, A. G. and Tweedie, R. L. (2012). Convergence of invariant measures of truncation approximations to Markov processes. Appl. Math. 3, 2205–2215.CrossRefGoogle Scholar
Kimura, M. and Takine, T. (2018). Computing the conditional stationary distribution in Markov chains of level-dependent M/G/1-type. Stoch. Models 34, 207–238.CrossRefGoogle Scholar
Latouche, G. and Ramaswami, V. (1999). Introduction to Matrix Analytic Methods in Stochastic Modeling. SIAM, Philadelphia, PA.CrossRefGoogle Scholar
Liu, Y., Li, W. and Masuyama, H. (2018). Error bounds for augmented truncation approximations of continuous-time Markov chains. Operat. Res. Lett. 46, 409–413.CrossRefGoogle Scholar
Masuyama, H. (2018). Limit formulas for the normalized fundamental matrix of the northwest-corner truncation of Markov chains: Matrix-infinite-product-form solutions of block-Hessenberg Markov chains. Preprint. Available at https://arxiv.org/pdf/1603.07787v7.pdf.Google Scholar
Nagamochi, H. (2018). Personal communication.Google Scholar
Neuts, M. F. (1981). Matrix-Geometric Solutions in Stochastic Models. Johns Hopkins University Press.Google Scholar
Neuts, M. F. (1989). Structured Stochastic Matrices of M/G/1 Type and Their Applications. Marcel Dekker, New York, NY.Google Scholar
Seneta, E. (1980). Computing the stationary distribution for infinite Markov chains. Linear Algebra Appl. 34, 259–267.CrossRefGoogle Scholar
Stewart, W. J. (1994). Introduction to the Numerical Solution of Markov Chains. Princeton University Press.Google Scholar
Takahashi, Y. (1975). A lumping method for numerical calculations of stationary distributions of Markov chains. Res. Rep. B-18, Department of Information Sciences, Tokyo Institute of Technology.Google Scholar
Takine, T. (2016). Analysis and computation of the stationary distribution in a special class of level-dependent M/G/1-type and its application to BMAP/M/ $\infty$ and BMAP/M/c+M queues. Queueing Systems 84, 49–77.CrossRefGoogle Scholar
Zhao, Y. Q. and Liu, D. (1996). The censored Markov chain and best augmentation. J. Appl. Prob. 33, 623–629.CrossRefGoogle Scholar