Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T11:29:42.462Z Has data issue: false hasContentIssue false
  • English
  • Français

Fluctuation identities for Omega-killed spectrally negative Markov additive processes and dividend problem

Part of: Stochastic processes

Published online by Cambridge University Press:  15 July 2020

Irmina Czarna ,
Adam Kaszubowski ,
Shu Li  and
Zbigniew Palmowski Open the ORCID record for Zbigniew Palmowski [Opens in a new window]
Irmina Czarna*
Affiliation:
Wrocław University of Science and Technology
Adam Kaszubowski*
Affiliation:
University of Wrocław
Shu Li*
Affiliation:
Western University
Zbigniew Palmowski*
Affiliation:
Wrocław University of Science and Technology
*
*Postal address: Faculty of Pure and Applied Mathematics, Hugo Steinhaus Centre, Wrocław University of Science and Technology, Poland
**Postal address: Mathematical Institute, University of Wrocław, Poland
***Postal address: Department of Statistical and Actuarial Sciences, Western University, Canada
*Postal address: Faculty of Pure and Applied Mathematics, Hugo Steinhaus Centre, Wrocław University of Science and Technology, Poland
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we solve exit problems for a one-sided Markov additive process (MAP) which is exponentially killed with a bivariate killing intensity 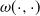$\omega(\cdot,\cdot)$ dependent on the present level of the process and the current state of the environment. Moreover, we analyze the respective resolvents. All identities are expressed in terms of new generalizations of classical scale matrices for MAPs. We also remark on a number of applications of the obtained identities to (controlled) insurance risk processes. In particular, we show that our results can be applied to the Omega model, where bankruptcy takes place at rate 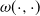$\omega(\cdot,\cdot)$ when the surplus process becomes negative. Finally, we consider Markov-modulated Brownian motion (MMBM) as a special case and present analytical and numerical results for a particular choice of piecewise intensity function 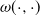$\omega(\cdot,\cdot)$ .

Keywords

Dividendsfluctuation theoryMarkov modulationOmega modelpotential measures

MSC classification

Primary: 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 60G17: Sample path properties
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 2 , June 2020 , pp. 404 - 432
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albrecher, H., Gerber, H. U. and Shiu, E. S. W. (2011). The optimal dividend barrier in the gamma-omega model. Eur. Actuar. J. 1, 43–55.CrossRefGoogle Scholar
Asmussen, S. (2003). Applied Probability and Queues, 2nd edn. Springer, New York.Google Scholar
Avram, F., Palmowski, Z. and Pistorius, M. R. (2007). On the optimal dividend problem for a spectrally negative Lévy process. Ann. Appl. Probab. 17, 156–180.CrossRefGoogle Scholar
Bellman, R. (1960). Introduction to Matrix Analysis. McGraw-Hill, New York–Toronto–London.Google Scholar
Breuer, L. (2012). Exit problems for reflected Markov-additive processes with phase-type jumps. J. Appl. Prob. 49, 697–709.CrossRefGoogle Scholar
D’Auria, B., Ivanovs, J., Kella, O. and Mandjes, M. (2010). First passage of a Markov additive process and generalized Jordan chains. J. Appl. Prob. 47, 1048–1057.CrossRefGoogle Scholar
Dieker, A. B. and Mandjes, M. (2011). Extremes of Markov-additive processes with one-sided jumps, with queueing applications. Methodol. Comput. Appl. Probab. 13, 221–267.CrossRefGoogle Scholar
Czarna, I. and Palmowski, Z. (2011). Ruin probability with Parisian delay for a spectrally negative Lévy risk process. J. Appl. Prob. 48, 984–1002.CrossRefGoogle Scholar
Czarna, I., Li, Y., Palmowski, Z. and Zhao, C. (2016). Optimal Parisian-type dividends payments discounted by the number of claims for the perturbed classical risk process. Preprint. Available at http://arxiv.org/abs/1603.06904.Google Scholar
De Finetti, B. (1957). Su un’impostazione alternativa della teoria collettiva del rischio. Trans. XV Intern. Congress Act. 2, 433–443.Google Scholar
Gerber, H. U., Shiu, E. S. W. and Yang, H. (2012). The Omega model: from bankruptcy to occupation times in the red. Eur. Actuar. J. 2, 259–272.CrossRefGoogle Scholar
Ivanovs, J. (2010). Markov-modulated Brownian motion with two reflecting barriers. J. Appl. Prob. 47, 1034–1047.CrossRefGoogle Scholar
Ivanovs, J. and Mandjes, M. (2010). First passage of time-reversible spectrally negative Markov additive processes. Operat. Res. Letters 38, 77–81.CrossRefGoogle Scholar
Ivanovs, J. (2011). One-sided Markov additive processes and related exit problems. Doctoral Thesis, University of Amsterdam. Uitgeverij BOXPress, Oisterwijk.Google Scholar
Ivanovs, J. and Palmowski, Z. (2012). Occupation densities in solving exit problems for Markov additive processes and their reflections. Stoch. Process. Appl. 122, 3342–3360.CrossRefGoogle Scholar
Ivanovs, J. (2014). Potential measures of one-sided Markov additive processes with reflecting and terminating barriers. J. Appl. Prob. 51, 1154–1170.CrossRefGoogle Scholar
Ivanovs, J. (2019). Spectrally-negative Markov additive processes in continuous time [MATHEMATICA package]. Available at https://sites.google.com/site/jevgenijsivanovs/files.Google Scholar
Kuznetsov, A., Kyprianou, A. E. and Rivero, V. (2012). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II (Lecture Notes in Mathematics, Vol. 2061), Springer, Berlin, Heidelberg.Google Scholar
Kyprianou, A. E. (2006). Introductory Lectures on Fluctuations of Lévy Processes with Applications. Springer, Berlin, Heidelberg.Google Scholar
Kyprianou, A. E. (2013). Gerber-Shiu Risk Theory. Springer, Berlin, Heidelberg.CrossRefGoogle Scholar
Kyprianou, A. E. and Palmowski, Z. (2008). Fluctuations of spectrally negative Markov additive processes. In Séminaire de Probabilité XLI, Springer, Berlin, pp. 121–135.CrossRefGoogle Scholar
Li, B. and Palmowski, Z. (2018). Fluctuations of omega-killed spectrally negative Lévy processes. Stoch. Process. Appl. 128, 3273–3299.CrossRefGoogle Scholar
Loeffen, R. (2008). On optimality of the barrier strategy in de Finetti’s dividend problem for spectrally negative Lévy processes. Ann. Appl. Prob. 18, 1669–1680.CrossRefGoogle Scholar
Loeffen, R. and Renaud, J. F. (2010). De Finetti’s optimal dividends problem with an affine penalty function at ruin. Insurance Math. Econom. 46, 98–108.CrossRefGoogle Scholar
Renaud, J. F. and Zhou, X. (2007). Distribution of the present value of dividend payments in a Lévy risk model. J. Appl. Prob. 44, 420–427.CrossRefGoogle Scholar