Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T16:52:48.747Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for stochastic growth models. I

Published online by Cambridge University Press:  01 July 2016

Harry Kesten
Harry Kesten*
Affiliation:
Cornell University
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider d-dimensional stochastic processes which take values in (R+)d. These processes generalize Galton-Watson branching processes, but the main assumption of branching processes, independence between particles, is dropped. Instead, we assume for some

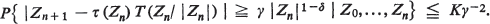Here τ: (R+)d → R+, |x| = Σ1d |x(i)| A = {x ∈ (R+)d: |x| = 1} and T: A → A. Under various assumptions on the maps τ and T it is shown that with probability one there exists a ρ > 1, a fixed point p ∈ A of T and a random variable w such that limn→∞Znρ−n = wp. This result is a generalization of the main limit theorem for super-critical branching processes; note, however, that in the present situation both p and ρ are random as well. The results are applied to a population genetical model for zygotic selection without mutation at one locus.

Keywords

GROWTH MODELSPOPULATION GROWTHEXPONENTIAL GROWTHMALTHUSIAN PARAMETERGROWTH RATEFIXED POINTPOPULATION COMPOSITIONCONVERGENCE OF COMPOSITION OF POPULATIONFISHER-WRIGHT-HALDANE MODEL
Type
Research Article
Information
Advances in Applied Probability , Volume 4 , Issue 2 , August 1972 , pp. 193 - 232
Copyright
Copyright © Applied Probability Trust 1972 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Baum, L. E., Petrie, T., Soules, G. and Weiss, N. (1970) A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann. Math. Statist. 41, 164–171.Google Scholar
[2] Breiman, L. (1968) Probability. Addison-Wesley, Reading, Mass.Google Scholar
[3] Blakley, G. R. (1964) The sequence of iterates of a non negative non-linear transformation. Bull. Amer. Math. Soc. 70, 712–715.Google Scholar
[4] Eilenberg, S. and Steenrod, N. (1952) Foundations of Algebraic Topology. Princeton Univ. Press, Princeton, N. J.CrossRefGoogle Scholar
[5] Feller, W. (1968) An Introduction to Probability Theory and its Applications. Vol. I, 3rd ed. John Wiley, New York.Google Scholar
[6] Karlin, S. (1962–63) Lectures on mathematical biology. Stanford University.Google Scholar
[7] Kesten, H. (1970) Quadratic transformations: a model for population growth. Adv. Appl. Prob. 2, 1–82 and 179–228.Google Scholar
[8] Kesten, H. (1971) Some nonlinear stochastic growth models. Bull. Amer. Math. Soc. 77, 492–511.CrossRefGoogle Scholar
[9] Kesten, H. and Stigum, B. P. Balanced growth under uncertainty in decomposable economies. Submitted to Econometrica. Google Scholar
[10] Li, C. C. (1967) Genetic equilibrium under selection. Biometrics 23, 397–484.Google Scholar
[11] Meyer, P. A. (1966) Probability and Potentials. Blaisdell, Waltham, Mass.Google Scholar
[12] Moran, P. A. P. (1962) The Statistical Processes of Evolutionary Theory. Clarendon Press, Oxford.Google Scholar
[13] Mulholland, H. P. and Smith, C. A. B. (1959) An inequality in genetical theory. Amer. Math. Monthly 66, 673–683.Google Scholar
[14] Ostrowski, A. M. (1966) Solutions of Equations and Systems of Equations. 2nd ed. Academic Press, New York.Google Scholar
[15] Scheuer, P. A. G. and Mandel, S. P. H. (1959) An inequality in population genetics. Heredity 31, 519–524.Google Scholar
[16] Smale, S. (1963) Stable manifolds for differential equations and diffeomorphisms. Ann. Scuola Norm. Sup. Pisa (3) 17, 97–116.Google Scholar
[17] Sternberg, S. (1957) Local contractions and a theorem of Poincaré. Amer. J. Math. 79, 809–824.CrossRefGoogle Scholar