Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T21:06:36.032Z Has data issue: false hasContentIssue false
  • English
  • Français

Speed and concentration of the covering time for structured coupon collectors

Part of: Designs and configurations Combinatorial probability Graph theory Stochastic processes

Published online by Cambridge University Press:  15 July 2020

Victor Falgas-Ravry ,
Joel Larsson Open the ORCID record for Joel Larsson [Opens in a new window]  and
Klas Markström
Victor Falgas-Ravry*
Affiliation:
Umeå Universitet
Joel Larsson*
Affiliation:
Warwick University
Klas Markström*
Affiliation:
Umeå Universitet
*
*Postal address: Department of Mathematics and Mathematical Statistics, Umeå Universitet. Email: victor.falgas-ravry@math.umu.se
**Postal address: Mathematics Institute, Warwick University. Email: joel.larsson@warwick.ac.uk
***Postal address: Department of Mathematics and Mathematical Statistics, Umeå Universitet. Email: klas.markström@math.umu.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Let V be an n-set, and let X be a random variable taking values in the power-set of V. Suppose we are given a sequence of random coupons 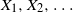$X_1, X_2, \ldots $ , where the 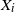$X_i$ are independent random variables with distribution given by X. The covering time T is the smallest integer 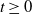$t\geq 0$ such that 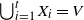$\bigcup_{i=1}^t X_i=V$ . The distribution of T is important in many applications in combinatorial probability, and has been extensively studied. However the literature has focused almost exclusively on the case where X is assumed to be symmetric and/or uniform in some way.

In this paper we study the covering time for much more general random variables X; we give general criteria for T being sharply concentrated around its mean, precise tools to estimate that mean, as well as examples where T fails to be concentrated and when structural properties in the distribution of X allow for a very different behaviour of T relative to the symmetric/uniform case.

Keywords

Coupon collectorconcentration inequalitiescombinatorial probability

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 05B40: Packing and covering 05C80: Random graphs 60G99: None of the above, but in this section
Type
Original Article
Information
Advances in Applied Probability , Volume 52 , Issue 2 , June 2020 , pp. 433 - 462
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achlioptas, D. and Naor, A. (2005). The two possible values of the chromatic number of a random graph. Ann. Math. 162, 1335–1351.CrossRefGoogle Scholar
Adler, I. and Ross, S. M. (2001). The coupon subset collection problem. J. Appl. Prob. 38, 737–746.10.1239/jap/1005091036CrossRefGoogle Scholar
Aldous, D. J. (1989). An introduction to covering problems for random walks on graphs. J. Theoret. Prob. 2, 87–89.10.1007/BF01048271CrossRefGoogle Scholar
Aldous, D. J. (1991). Threshold limits for cover times. J. Theoret. Prob. 4, 197–211.10.1007/BF01047002CrossRefGoogle Scholar
Barbour, A. D. and Holst, L. (1989). Some applications of the Stein-Chen method for proving Poisson convergence. Adv. Appl. Prob. 21, 74–90.CrossRefGoogle Scholar
Baum, L. E. and Billingsley, P. (1965). Asymptotic distributions for the coupon collector’s problem. Ann. Math. Statist. 36, 1835–1839.CrossRefGoogle Scholar
Bollobás, B. and Thomason, A. G. (1987). Threshold functions. Combinatorica 7, 35–38.CrossRefGoogle Scholar
Borcea, J., Brändén, P. and Liggett, T. (2009). Negative dependence and the geometry of polynomials. J. Amer. Math. Soc. 22, 521–567.CrossRefGoogle Scholar
Chung, F. and Lu, L. (2006). Complex Graphs and Networks (CBMS Regional Conference Series in Mathematics 107). American Mathematical Society, Providence, RI.10.1090/S0002-9947-05-04023-7Google Scholar
Chvátal, V. (1991). Almost all graphs with 1.44n edges are 3-colorable. Random Structures Algorithms 2, 11–28.CrossRefGoogle Scholar
Coja-Oghlan, A. (2014). The asymptotic k-SAT threshold. In STOC ’14: Proceedings of the 46th Annual ACM Symposium on Theory of Computing, Association for Computing Machinery, New York, pp. 804–813.CrossRefGoogle Scholar
De Moivre, A. (1711). De mensura sortis, seu, de probabilitate eventuum in ludis a casu fortuito pendentibus. Phil. Trans. R. Soc. London A 27, 213–264.Google Scholar
Ding, J., Sly, A. and Sun, N. (2015). Proof of the satisfiability conjecture for large k. In STOC ’15: Proceedings of the 47th Annual ACM Symposium on Theory of Computing, Association for Computing Machinery, New York, pp. 59–68.10.1145/2746539.2746619CrossRefGoogle Scholar
Dubois, O., Boufkhad, Y. and Mandler, J. (2000). Typical random 3-SAT formulae and the satisfiability threshold. In SODA ’00: Proceedings of the Eleventh Annual ACM-SIAM Symposium on Discrete Algorithms, Society for Industrial and Applied Mathematics, Philadelphia, pp. 126–127.Google Scholar
Eicker, P. J., Siddiqui, M. M. and Mielke, P. W. (1972). A matrix occupancy problem. Ann. Math. Statist. 43, 988–996.CrossRefGoogle Scholar
Erdős, P. and Rényi, A. (1961). On a classical problem of probability theory. Publ. Math. Inst. Hungar. Acad. Sci 6, 215–220.Google Scholar
Erdős, P. and Rényi, A. (1960). On the evolution of random graphs. Publ. Math. Inst. Hungar. Acad. Sci 5, 17–61.Google Scholar
Falgas-Ravry, V. and Walters, M. (2012). Sharpness in the k-nearest-neighbours random geometric graph model. Adv. Appl. Prob. 44, 617–634.CrossRefGoogle Scholar
Feder, T. and Mihail, M. (1992). Balanced matroids. In STOC ’92: Proceedings of the Twenty-fourth Annual ACM Symposium on Theory of Computing, Association for Computing Machinery, New York, pp. 26–38.10.1145/129712.129716CrossRefGoogle Scholar
Feller, W. (1950). An Introduction to Probability Theory and Its Applications, Vol. 1. John Wiley, New York.Google Scholar
Ferrante, M. and Frigo, N. (2012). A note on the coupon-collector’s problem with multiple arrivals and the random sampling. Preprint. Available at http://arxiv.org/abs/1209.2667.Google Scholar
Flajolet, P., Gardy, D. and Thimonier, L. (1992). Birthday paradox, coupon collectors, caching algorithms and self-organizing search. Discrete Appl. Math. 39, 207–229.10.1016/0166-218X(92)90177-CCrossRefGoogle Scholar
Frieze, A. and Wormald, N. (2005). Random k-SAT: a tight threshold for moderately growing k. Combinatorica 25, 297–305.10.1007/s00493-005-0017-3CrossRefGoogle Scholar
Gittelsohn, A. M. (1969). An occupancy problem. Amer. Statistician 23, 11–12.Google Scholar
Hall, P. (1988). Introduction to the Theory of Coverage Processes. John Wiley, New York.Google Scholar
Holst, L. (1977). Some asymptotic results for occupancy problems. Ann. Prob. 5, 1028–1035.10.1214/aop/1176995671CrossRefGoogle Scholar
Holst, L. (1986). On birthday, collectors’, occupancy and other classical urn problems. Internat. Statist. Rev. 54, 15–27.10.2307/1403255CrossRefGoogle Scholar
Huillet, T. (2003). Sampling problems for randomly broken sticks. J. Phys. A 36, 3947.10.1088/0305-4470/36/14/302CrossRefGoogle Scholar
Ivanov, V. A., Ivchenko, G. I. and Medvedev, Y. I. (1985). Discrete problems in probability theory. J. Soviet Math. 31, 2759–2795.10.1007/BF02116601CrossRefGoogle Scholar
Ivchenko, G. I. (1998). How many samples does it take to see all the balls in an urn? Math. Notes 64, 49–54.10.1007/BF02307195CrossRefGoogle Scholar
Janson, S. (1986). Random coverings in several dimensions. Acta Math. 156, 83–118.CrossRefGoogle Scholar
Johnson, B. C. and Sellke, T. M. (2010). On the number of iid samples required to observe all of the balls in an urn. Methodology Comput. Appl. Prob. 12, 139–154.10.1007/s11009-008-9095-1CrossRefGoogle Scholar
Johnson, N. L. and Kotz, S. (1977). Urn Models and Their Application: An Approach to Modern Discrete Probability Theory. John Wiley, New York.Google Scholar
Kaporis, A. C. et al. (2001). Coupon collectors, q-binomial coefficients and the unsatisfiability threshold. In Theoretical Computer Science (ICTCS 2001) (Lecture Notes in Computer Science 2202), Springer, Berlin, Heidelberg, pp. 328–338.CrossRefGoogle Scholar
Khakimullin, E. R. and Enatskaya, N. Y. (1997). Limit theorems for the number of empty cells. Discrete Math. Appl. 7, 209–220.10.1515/dma.1997.7.2.209CrossRefGoogle Scholar
Kingman, J. F. C. (1978). Random partitions in population genetics. Proc. R. Soc. London A 361, 1–20.Google Scholar
Kobza, J. E., Jacobson, S. H. and Vaughan, D. E. (2007). A survey of the coupon collector’s problem with random sample sizes. Methodology Comput. Appl. Prob. 9, 573–584.10.1007/s11009-006-9013-3CrossRefGoogle Scholar
Kolchin, V. F., Sevast’yanov, B. A. and Chistyakov, V. P. (1978). Random Allocations. V. H. Winston, Washington, DC.Google Scholar
Laplace, P.-S. (1774). Mémoire sur les suites récurro-récurrentes et sur leurs usages dans la théorie des hasards. Mém. Acad. Roy. Sci. Paris 6, 353–371.Google Scholar
Larsson, J. and Markström, K. (2019). Biased random k-SAT. Preprint. Available at http://arxiv.org/abs/1906.05127.Google Scholar
Mantel, N. and Pasternack, B. S. (1968). A class of occupancy problems. Amer. Statistician 22, 23–24.Google Scholar
McKay, B. D. and Skerman, F. (2013). Degree sequences of random digraphs and bipartite graphs. Preprint. Available at http://arxiv.org/abs/1302.2446.Google Scholar
Mézard, M. and Zecchina, R. (2002). Random K-satisfiability problem: From an analytic solution to an efficient algorithm. Phys. Rev. E 66, 056126.CrossRefGoogle Scholar
Mikhailov, V. G. (1978). An estimate of the rate of convergence to the Poisson distribution in group allocation of particles. Theory Prob. Appl. 22, 554–562.10.1137/1122065CrossRefGoogle Scholar
Neal, P. and Moriary, J. (2009). Sampling efficiency and biodiversity. Research Report No. 9, University of Manchester Probability and Statistics Group.Google Scholar
Newman, D. J. and Shepp, L. (1960). The double dixie cup problem. Amer. Math. Monthly 67, 58–61.10.2307/2308930CrossRefGoogle Scholar
Papanicolaou, V. G., Kokolakis, G. E. and Boneh, S. (1998). Asymptotics for the random coupon collector problem. J. Computat. Appl. Math. 93, 95–105.CrossRefGoogle Scholar
Patil, G. P. and Taillie, C. (1977). Diversity as a concept and its implications for random environments. Bull. Internat. Statist. Inst. 4, 497–515.Google Scholar
Poli, R. (2005). Tournament selection, iterated coupon-collection problem, and backward-chaining evolutionary algorithms. In Foundations of Genetic Algorithms, Springer, Berlin, Heidelberg, pp. 132–155.CrossRefGoogle Scholar
Pólya, G. (1930). Eine Wahrscheinlichkeitsaufgabe in der Kundenwerbung. Z. Angew. Math. Me. 10, 96–97.10.1002/zamm.19300100113CrossRefGoogle Scholar
Poon, A., Davis, B. H. and Chao, L. (2005). The coupon collector and the suppressor mutation estimating the number of compensatory mutations by maximum likelihood. Genetics 170, 1323–1332.CrossRefGoogle ScholarPubMed
Raab, M. and Steger, A. (1998). Balls into Bins – a simple and tight analysis. In Randomization and Approximation Techniques in Computer Science, Springer, Berlin, Heidelberg, pp. 159–170.10.1007/3-540-49543-6_13CrossRefGoogle Scholar
Sarkar, A. and Haenggi, M. (2013). Secrecy coverage. Internet Math. 9, 199–216.CrossRefGoogle Scholar
Savage, S., Wetherall, D., Karlin, A. and Anderson, T. (2001). Network support for IP traceback. IEEE/ACM Trans. Networking 9, 226–237.10.1109/90.929847CrossRefGoogle Scholar
Sellke, T. M. (1995). How many iid samples does it take to see all the balls in a box? Ann. Appl. Prob. 5, 294–309.10.1214/aoap/1177004841CrossRefGoogle Scholar
Sprott, D. A. (1969). A note on a class of occupancy problems. Amer. Statistician 23, 12–13.Google Scholar
Stadje, W. (1990). The collector’s problem with group drawings. Adv. Appl. Prob. 22, 866–882.CrossRefGoogle Scholar
Vasudevan, S., Towsley, D., Goeckel, D. and Khalili, R. (2009). Neighbor discovery in wireless networks and the coupon collector’s problem. In Proceedings of the 15th Annual International Conference on Mobile Computing and Networking (MobiCom ’09), Association for Computing Machinery, New York, pp. 181–192.CrossRefGoogle Scholar
Vatutin, V. A. and Mikhailov, V. G. (1983). Limit theorems for the number of empty cells in an equiprobable scheme for group allocation of particles. Theory Prob. Appl. 27, 734–743.CrossRefGoogle Scholar