Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T06:48:53.586Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurements of Dynamic Stability Derivatives of Hyperballistic and Conic Shapes at M = 6.85

Published online by Cambridge University Press:  07 June 2016

A.M.S. Qasrawi  and
R.A. East
A.M.S. Qasrawi
Affiliation:
Projects: Lucas Research Centre, West Midlands
R.A. East
Affiliation:
Department of Aeronautics and Astronautics, Southampton University
Get access

Summary

Experimental measurement of the pitching stability derivatives 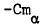and 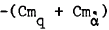of AGARD hyperballistic standard models HB1 and HB2, a hemisphere-cylinder double flared configuration designated HBS and three 10° semi angle cones of bluntness ratios 0.0, 0.2 and 0.4 are reported. Data were obtained at a Mach number of 6.85 in a short duration light piston tunnel using the small amplitude free oscillation technique. The tests were conducted at Reynolds numbers from 0.2 × 106 to 0.85 × 106, based on centre-body diameter, for the hyperballistic shapes and from 1.45 × 1016 to 2.17 × 106, based on base diameter, for the conical shapes. The mean angle of attack was varied from 0 to 17.0 degrees and the frequency parameter from 0.0020 to 0.0043 for the hyperballistic shapes and from 0.0018 to 0.0092 for the cones. All models tested were found to be dynamically stable for all positions of the axis of oscillation considered. The significant observed non linear variations of the damping derivative with angle of attack for the 0.2 and 0.4 bluntness cones and the HB2 shape could be partially accounted for qualitatively by boundary layer transition induced effects. The variation of the derivatives with angle of attack for the pointed cone were consistent with a fully turbulent boundary layer, whereas it was probable that for the HB1 and HBS models the boundary layer remained laminar throughout. Variation of the frequency parameter resulted in no significant effect on the measured stability derivatives.

Type
Research Article
Information
Aeronautical Quarterly , Volume 32 , Issue 1 , February 1981 , pp. 1 - 30
Copyright
Copyright © Royal Aeronautical Society. 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Gray, J.D., Summary Report on Aerodynamic Characteristics of Standard Models HB1 and HB2. Arnold Engineering Development Centre, AEDC-TDR-64-137, 1964 Google Scholar
2 Sibley, G.O., Dynamic Stability Tests of AGARD Models HB1 and HB2 in a Blowdown Tunnel at Mach 5.4. Von Karman Institute of Fluid Dynamics, VKI PR 65 - 141, 1965.Google Scholar
3 Ericsson, L.E., Unsteady Embedded Newtonian Flow. Astronautica Acta, Vol XVIII, Number 5, p 309–330, 1973.Google Scholar
4 Jones, T.V., Schultz, D.L. and Hendley, A.D., On the Flow in an Isentropic Light Piston Tunnel. ARC R & M 3731, 1973.Google Scholar
5 Qasrawi, A.M.S., Measurements of Hypersonic Dynamic Stability of Pitching Blunt-Nosed Bodies in a Short-Duration Facility. Ph.D. Thesis, Southampton University, p 70–74, 1978.Google Scholar
6 Ward, L.K., Influence of Boundary Layer Transition on Dynamic Stability at Hypersonic Speeds. Paper 9, Vol. II, Transactions of the Second Technical Workshop on Dynamic Stability Testing, AEDC, 1965.Google Scholar
7 Khalid, M., A Theoretical and Experimental Study of the Hypersonic Dynamic Stability of Blunt Axi-symmetric Conical and Power-Law Shaped Bodies. Ph.D. Thesis, Southampton University, p 88–91, 1978.Google Scholar
8. Uselton, B.L., Freeman, D.C. Jr. and Boyden, R.P., Experimental Dynamic Stability Characteristics of a Shuttle Orbiter at M∞ = 8. Journal of Spacecraft and Rockets, Volume XIII, Number 10, p 635–640, 1976.Google Scholar
9. Morrison, A.M. and Ingram, C.W., Stability Coefficients of a Missile at Angles of Attack. Journal of Spacecraft and Rockets, Volume XIII, Number 5, p 318–319, 1976.Google Scholar
10. Uselton, J.C. and Uselton, B.L., Validity of Small Amplitude Oscillation Dynamic Stability Measurement Technique. Journal of Spacecraft and Rockets, Volume XIII, Number 5, p 266–270, 1976.CrossRefGoogle Scholar
11. Schueler, C.J., Ward, L.K. and Hodapp, A.E. Jr. Techniques for the Measurement of Dynamic Stability Derivatives in Ground Test Facilities. AGARDograph 121, 1967.Google Scholar
12. East, R.A. and Qasrawi, A.M.S., A Long Stroke Isentropic Free Piston Hypersonic Wind Tunnel. Aero. Res. Council. R&M 3844, 1980.Google Scholar