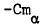Experimental measurement of the pitching stability derivatives and 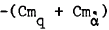of AGARD hyperballistic standard models HB1 and HB2, a hemisphere-cylinder double flared configuration designated HBS and three 10° semi angle cones of bluntness ratios 0.0, 0.2 and 0.4 are reported. Data were obtained at a Mach number of 6.85 in a short duration light piston tunnel using the small amplitude free oscillation technique. The tests were conducted at Reynolds numbers from 0.2 × 106 to 0.85 × 106, based on centre-body diameter, for the hyperballistic shapes and from 1.45 × 1016 to 2.17 × 106, based on base diameter, for the conical shapes. The mean angle of attack was varied from 0 to 17.0 degrees and the frequency parameter from 0.0020 to 0.0043 for the hyperballistic shapes and from 0.0018 to 0.0092 for the cones. All models tested were found to be dynamically stable for all positions of the axis of oscillation considered. The significant observed non linear variations of the damping derivative with angle of attack for the 0.2 and 0.4 bluntness cones and the HB2 shape could be partially accounted for qualitatively by boundary layer transition induced effects. The variation of the derivatives with angle of attack for the pointed cone were consistent with a fully turbulent boundary layer, whereas it was probable that for the HB1 and HBS models the boundary layer remained laminar throughout. Variation of the frequency parameter resulted in no significant effect on the measured stability derivatives.

The linearised time dependent momentum integral equation is used in conjunction with assumed velocity profiles and a quasi-static skin friction approximation to predict the turbulent boundary layer response to sinusoidal streamwise velocity fluctuations in the freestream. The mean zero pressure gradient case, corresponding to flat plate flow, is presented in detail and verified by comparison with experimental data and alternative calculations. The asymptotic turbulent boundary layer response to very high frequency perturbations is also derived. It is shown that a travelling wave component in the freestream, with its associated time dependent streamwise pressure gradient, has a dominant effect on the turbulent boundary layer response.

Earlier analysis, Middleton, of the laminar discharge of a ‘strong’ incompressible jet, due to a line or point source of momentum, into an unbounded co-flowing stream of the same density, is extended to the case of plane and round ‘weak’ jets the velocity in which only slightly exceeds the ambient velocity. In addition to recovering Goldstein’s solutions for ‘wake-like’ flows, use of the momentum integral equation provides approximate relationships for the decay of the centre velocities from the strong to the weak situations. Comparison is made with Wygnanski’s perturbation approach, suitably extended, and it is concluded that for the plane jet case, for which the agreement is better, the curve for the centre-plane velocity is correct to within about 12% throughout its range. The present approach is applicable to any flow for which a similarity solution exists as a first order solution, and is especially suitable when two such solutions exist for large and small values of an appropriate parameter. Its use also throws light on the form to be adopted for a perturbation expansion.

A brief description is given of an accurate numerical method for the inverse calculation of both attached and separated laminar, two-dimensional, incompressible boundary-layers with prescribed displacement thickness. The method employs downstream-marching, using an approximation to the convection terms in the reverse-flow region to stabilise the computation. Results of three calculations made by this method, using measured distributions of displacement thickness as input, are presented and compared with the corresponding measured velocity profiles and distributions of external velocity. Very close agreement between theory and experiment is found in general, giving further evidence of the validity of the boundary-layer approximation in separated flows of limited extent.

A numerical method for computing potential flow through either a planar or axisymmetric nozzle is described. Some results obtained from a computer program based on this method are presented and compared with experimental data.

Simple, yet reasonably accurate, expressions have been developed for the prediction of skin friction and heat transfer coefficient at an infinite swept attachment line using the concepts of ‘reference temperature’ and ‘Reynolds analogy’. The formulae have then been used to investigate the effect of varying sweep angle with constant undisturbed free stream conditions in the limits of very low and very high Mach number.

This note presents the results of an experimental investigation of the flow over a simple delta wing designed for a Mach number of 3.5. Complete pressure distributions were measured for incidences of 0°, 10° and 20° at Mach numbers of 2.5 and 3.5. A number of schlieren photographs of the shock system around the wing were obtained at the same conditions and surface streamline patterns were studied at M = 3.5. The measurements were made to support numerical calculations which use this wing as a test case.

The fluctuating loading on a cylindrical bluff body due to vortex shedding increases if the body is capable of vibration. This is a result of amplification of the fluctuating pressures around a two-dimensional section of the body together with an improvement of the spanwise correlation of the vortex shedding. Measurement of the fluctuating forces on the cylinder during this process gives no guide as to the relative magnitude of these effects. In this paper, root mean square fluctuating pressure distributions and pressure correlations across a chord are presented for a square cylinder with front face normal to the approach flow whilst stationary and during forced vibration. The fluctuating lift coefficient for a two-dimensional section of the cylinder and its maximum amplification during vibration are calculated.

A method is described for calculating numerically the aerodynamic stiffness and damping coefficients and loading distributions for a two-dimensional thin aerofoil oscillating harmonically in subsonic flow, from the Possio Integral Equation by approximating the loading by a finite series of basis functions. Sample loading distributions obtained by using the method are presented for a Mach number of 0.9 and a frequency parameter of 0.4.

If two small fences are arranged approximately at right angles in plan view, the magnitude and direction of surface shear stress can be deduced from measurements of the pressure difference across each fence. Fence heights as small as 0.05 mm are easily achieved. The device is simpler to use than null-seeking arrangements, and is accurate even in the presence of strong pressure gradients, which are shown to have large effects on other types of surface obstacle in three-dimensional flow.

A two parameter approximate solution is presented for the flow along a streamwise corner having large, possibly infinite, curvature in its region of transition between the two quarter infinite planes which form its asymptotes. The two parameters are the angle between the asymptotes and a quantity proportional to the ratio of the local two-dimensional boundary layer thickness and the radius of curvature of the corner at the symmetry plane. Relative to the corner of infinite curvature (sharp corner) a finite curvature always tends to modify the solution towards that for a flat plate. This implies that for corner angles less than 180° the corner layer thickness in the symmetry plane is less than that for the sharp corner of the same angle and the shear stress is higher, the converse holding for angles greater than 180°. The flow in planes normal to the free stream direction is rather complex and typically there is a reversal in its direction within the symmetry plane.

The influence of spanwise correlation of fluctuating pressures due to vortex shedding on the total oscillatory loading of a long bluff cylinder in cross-flow is considered. Experimentally determined pressure correlation lengths on a stationary and vibrating cylinder of square cross section are then combined with previously obtained chordwise pressure distributions to demonstrate the amplification of the oscillatory lift on a long bluff cylinder during cross-flow vibrations.

A discrete-vortex representation of the wake of a circular cylinder, in which vortices are convected in a potential-flow calculation and maintain their identities unless they approach one another or a surface closely, predicts many of the unsteady flow features and is computationally more efficient than other schemes. The mean rate of shedding of vorticity is adjusted to be compatible with experiments at a high subcritical Reynolds number of 3 × 104 and the model gives reasonable predictions of separation, drag, lift, Strouhal number and vorticity loss in the formation region. The method is extended to accommodate a second cylinder and many of the surprising features which have been observed experimentally with two cylinders in a side-by-side arrangement are reproduced.

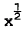The singular behaviour of an incompressible boundary layer at separation has been well established by the works of Howarth (1938), Goldstein (1948), Stewartson (1958), Curie (1958) and Terrill (1960). Stewartson (1962) remarked that the existence of the singularity at separation can be regarded as fully established and understood. The skin friction vanishes like where x is the distance to separation, and the stream function close to the wall is described by a series of powers of 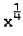, with coefficients that are functions of 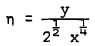, where y measures distance normal to the wall. At some stages in the expansion of the stream function, terms in log x have to be included. The case of the compressible flow is less satisfactory. Stewartson (1962) was unable to establish singularity at separation and concluded that the general compressible boundary layer cannot have a singularity at separation unless there is no heat transfer from the wall. This has been contradicted by the works of Merkin (1968) and Buckmaster (1970). Curie (1958) also reported that the difficulty encountered in computing the temperature field right down to the point of separation might be due to the singularity there. In this paper, the Goldstein-Stewart son approach is applied to laminar boundary layer flow at low speeds in which density is sensibly constant and the Prandtl number σ is taken as unity. Singularity is established at separation for the temperature field. The heat transfer does not vanish at separation point and is of the form

An analysis is made of the general two-cell thin-walled cylindrical tube subjected to longitudinal tension, bending and torsion. The walls of the tube may be of fibre composite with an asymmetric lay-up resulting in a coupling between direct and shear stresses and strains. The two-cell tube differs from the single-cell tube in that the tension axis and the principal axes of bending are not necessarily aligned to the c.g. and the principal moments of inertia of the longitudinal stress bearing material.

The quasi-one-dimensional theory due to Carpenter and Johannesen is applied to supercritical swirling flows in convergent-divergent nozzles. Only flows with uniformly constant stagnation pressure and entropy are considered. Values of exit impulse function and area ratio are given for various types of swirling flow with a range of back-pressure ratios. Thrust coefficients are calculated using these values and specific thrust coefficients plotted against maximum swirl velocity for various cases. In some cases the specific thrust for swirling nozzle flows very slightly exceeds the no-swirl value. The effects of nozzle wall curvature and flight speed on swirling nozzle flows are discussed. The contribution of post-exit thrust to the total thrust is estimated for swirling flow. Finally, the implications are considered of using swirl at the cruise conditions of a typical SST.

A measurement of the pressure distributions on D-section prisms over wide ranges of depth to height ratio and incidence in a smooth and in a turbulent flow was made with particular reference to the onset of transverse galloping. Good correlation between the onset of galloping and the critical depth, established already for rectangular and the related prisms with sharp downstream corners, applied also to D-section prisms both in a smooth and in a turbulent flow. The development of a reattachment type pressure distribution on the side face of the prism as the critical depth is reached is responsible for this correlation. There is very little effect of turbulence on the pressure distribution and the Strouhal number of a D-section prism with a depth to height ratio of 0.5.

The Nonlinear Magnus effect on the nutational oscillations of a missile has been studied. In particular the existence of self-sustained vibrations has been proved. A numerical method is suggested to obtain the limit cycles wherever they exist.

A method is given for the calculation of incompressible, inviscid flow through an axi-symmetric contracting duct for which the two dimensional flow with the same meridianal boundaries is known. The method, which is based on Whitehead, Wu and Waters original proposal, assumes that the contraction consists of two separate portions, upstream and downstream respectively. The flow in each portion is calculated and the two portions matched to produce a contraction of given area ratio with preassigned values of the two dimensional ‘overshoot’ and ‘undershoot’ parameters. It is worth emphasizing that in practice it is only necessary to do the calculations once to predict wall velocities for a family of contraction shapes with different area ratios provided they share a common upstream or downstream portion. The results given here show reasonable agreement with the pressure coefficients obtained in experiment for the upstream end of a small scale contraction of area ratio 16:1. There is however a discrepancy between theory and experiment at the downstream end and a qualitative explanation is advanced for this.

The subject of this paper is the effect of a disturbance to the turbulence structure of the flow on the reading of a Preston tube used to measure wall shear stress. Two kinds of disturbance have been studied experimentally, one caused by reattachment and the other by an abrupt change in wall roughness. The apparent wall shear stress measured by the Preston tube both in channel and boundary layer flows with these kinds of disturbance has been compared with the wall shear stress measured by a sublayer fence. The results give an idea of the magnitude of the error that is likely to arise when the Preston tube is used in a flow with disturbed turbulence structure.