Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T16:25:51.020Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTRIBUTED PROXIMAL-GRADIENT METHOD FOR CONVEX OPTIMIZATION WITH INEQUALITY CONSTRAINTS

Published online by Cambridge University Press:  18 November 2014

JUEYOU LI ,
CHANGZHI WU ,
ZHIYOU WU ,
QIANG LONG  and
XIANGYU WANG
JUEYOU LI
Affiliation:
School of Mathematics, Chongqing Normal University, Chongqing 400047, PR China email zywu@cqnu.edu.cn School of SITE, Federation University Australia, VIC 3353, Australia email lijueyou@163.com
CHANGZHI WU
Affiliation:
Australasian Joint Research Centre for Building Information Modelling, School of Built Environment, Curtin University, WA 6102, Australia email c.wu@curtin.edu.au
ZHIYOU WU*
Affiliation:
School of Mathematics, Chongqing Normal University, Chongqing 400047, PR China email zywu@cqnu.edu.cn
QIANG LONG
Affiliation:
School of Science, Southwest University of Science and Technology, Sichuan 621010, PR China email longqiang@swust.edu.cn
XIANGYU WANG
Affiliation:
Australasian Joint Research Centre for Building Information Modelling, School of Built Environment, Curtin University, WA 6102, Australia email c.wu@curtin.edu.au Department of Housing and Interior Design, Kyung Hee University, Seoul, Korea email x.wang@curtin.edu.au
*
✉zywu@cqnu.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a distributed optimization problem over a multi-agent network, in which the sum of several local convex objective functions is minimized subject to global convex inequality constraints. We first transform the constrained optimization problem to an unconstrained one, using the exact penalty function method. Our transformed problem has a smaller number of variables and a simpler structure than the existing distributed primal–dual subgradient methods for constrained distributed optimization problems. Using the special structure of this problem, we then propose a distributed proximal-gradient algorithm over a time-changing connectivity network, and establish a convergence rate depending on the number of iterations, the network topology and the number of agents. Although the transformed problem is nonsmooth by nature, our method can still achieve a convergence rate, 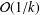${\mathcal{O}}(1/k)$, after 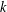$k$ iterations, which is faster than the rate, 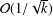${\mathcal{O}}(1/\sqrt{k})$, of existing distributed subgradient-based methods. Simulation experiments on a distributed state estimation problem illustrate the excellent performance of our proposed method.

Keywords

90C25distributed algorithmproximal-gradient methodexact penalty function methodconvex optimization
Type
Research Article
Information
The ANZIAM Journal , Volume 56 , Issue 2 , October 2014 , pp. 160 - 178
Copyright
Copyright © 2014 Australian Mathematical Society 

References

Beck, A. and Teboulle, M., “A fast iterative shrinkage-thresholding algorithm for linear inverse problems”, SIAM J. Imaging Sci. 2 (2009) 183–202; doi:10.1137/080716542.Google Scholar
Bertsekas, D. P., “Necessary and sufficient conditions for a penalty method to be exact”, Math. Program. 9 (1975) 87–99; doi:10.1007/bf01681332.CrossRefGoogle Scholar
Bertsekas, D. P., Nonlinear programming (Athena Scientific, Belmount, MA, 1999).Google Scholar
Bertsekas, D. P., “Incremental proximal methods for large scale convex optimization”, Math. Program. 129 (2011) 163–195; doi:10.1007/s1010701104720.Google Scholar
Bertsekas, D. P. and Tsitsiklis, J. N., Parallel and distributed computation: numerical methods (Prentice Hall, Englewood Cliffs, NJ, 1989).Google Scholar
Chen, A. I. and Ozdaglar, A., “A fast distributed proximal-gradient method”, in: 50th Annual Allerton Conference on Communication, Control and Computing, Allerton, New York, 2012 (IEEE, 2012) 601–608; doi:10.1109/allerton.2012.6483273.Google Scholar
de Oliveira, L. B. and Camponogara, E., “Multi-agent model predictive control of signaling split in urban traffic networks”, Transport. Res. Part C: Emerg. Tech. 8 (2010) 120–139; doi:10.1016/j.trc.2009.04.022.CrossRefGoogle Scholar
Duchi, J. C., Agarwal, A. and Wainwright, M. J., “Dual averaging for distributed optimization: convergence analysis and network scaling”, IEEE Trans. Automat. Control 57 (2012) 592–606; doi:10.1109/tac.2011.2161027.Google Scholar
Ebrahimian, R. and Baldick, R., “State estimation distributed processing”, IEEE Trans. Power Syst. 15 (2000) 1240–1246; doi:10.1109/59.898096.CrossRefGoogle Scholar
Johansson, B., Keviczky, T., Johansson, M. and Johansson, K. H., “Subgradient methods and consensus algorithms for solving convex optimization problems”, in: Proceedings of the 47th IEEE Conference on Decision Control, Cancun, Mexico, 2008 (IEEE, 2008) 4185–4190; doi:10.1109/cdc.2008.4739339.Google Scholar
Li, J., Wu, C., Wu, Z. and Long, Q., “Gradient-free method for nonsmooth distributed optimization”, J. Global. Optim. (2014) 1–16; doi:10.1007/s10898-014-0174-2.Google Scholar
Loxton, R., Lin, Q. and Teo, K. L., “Minimizing control variation in nonlinear optimal control”, Automatica 49 (2013) 2652–2664; doi:10.1016/j.automatica.2013.05.027.Google Scholar
Ma, C., Li, X., Yiu, K. F. C., Yang, Y. and Zhang, L., “On an exact penalty function method for semi-infinite programming problems”, J. Ind. Manag. Optim. 8 (2012) 705–726; doi:10.3934/jimo.2012.8.705.Google Scholar
Meng, Z., Hu, Q. and Dang, C., “A penalty function algorithm with objective parameters for nonlinear mathematical programming”, J. Ind. Manag. Optim. 5 (2009) 585–601; doi:10.3934/jimo.2009.5.585.CrossRefGoogle Scholar
Necoara, I., Nedelcu, V. and Dumitrache, I., “Parallel and distributed optimization methods for estimation and control in networks”, J. Process Control 21 (2011) 756–766; doi:10.1016/j.jprocont.2010.12.010.CrossRefGoogle Scholar
Nedic, A. and Bertsekas, D. P., “Incremental subgradient methods for nondifferentiable optimization”, SIAM J. Optim. 12 (2001) 109–138; doi:10.1137/s1052623499362111.Google Scholar
Nedic, A. and Ozdaglar, A., “Distributed subgradient methods for multi-agent optimization”, IEEE Trans. Automat. Control 54 (2009) 48–61; doi:10.1109/tac.2008.2009515.Google Scholar
Nedic, A. and Ozdaglar, A., “Subgradient methods for saddle-point problems”, J. Optim. Theory Appl. 142 (2009) 205–228; doi:10.1007/s1095700995227.Google Scholar
Nedic, A., Ozdaglar, A. and Parrilo, P. A., “Constrained consensus and optimization in multi-agent networks”, IEEE Trans. Automat. Control 55 (2010) 922–938; doi:10.1109/tac.2010.2041686.CrossRefGoogle Scholar
Nesterov, Y., “Gradient methods for minimizing composite functions”, Math. Program. 140 (2013) 125–161; doi:10.1007/s1010701206295.Google Scholar
Schmidt, M., Roux, N. L. and Bach, F. R., “Convergence rates of inexact proximal-gradient methods for convex optimization”, Adv. Neural Inf. Process. Syst. (2011) 1458–1466; arXiv:1109.2415.Google Scholar
Shen, Y., Zhang, W. and He, B., “Relaxed augmented Lagrangian-based proximal point algorithms for convex optimization with linear constraints”, J. Ind. Manag. Optim. 10 (2014) 743–759; doi:10.3934/jimo.2014.10.743.Google Scholar
Srikant, R., The mathematics of Internet congestion control (Springer, Berlin, 2004).CrossRefGoogle Scholar
Tsitsiklis, J. N., “Problems in decentralized decision making and computation”, Technical Report, DTIC Document, 1984.Google Scholar
Venkat, A. N., “Distributed model predictive control: theory and applications”, Ph. D. Thesis, CiteSeer, 2006.Google Scholar
Wu, C., Teo, K. L. and Wu, S. Y., “Minmax optimal control of linear systems with uncertainty and terminal state constraints”, Automatica 49 (2013) 1809–1815; doi:10.1016/j.automatica.2013.02.052.CrossRefGoogle Scholar
Xiao, L. and Boyd, S., “Fast linear iterations for distributed averaging”, Systems Control Lett. 53 (2004) 65–78; doi:10.1016/j.sysconle.2004.02.022.Google Scholar
Xiao, L., Boyd, S. and Kim, S. J., “Distributed average consensus with least-mean-square deviation”, J. Parallel Distrib. Comput. 67 (2007) 33–46; doi:10.1016/j.jpdc.2006.08.010.Google Scholar
Xiao, Y., Wu, S. Y. and He, B., “A proximal alternating direction method for l2-norm least squares problem in multi-task feature learning”, J. Ind. Manag. Optim. 8 (2012) 1057–1069; doi:10.3934/jimo.2012.8.1057.CrossRefGoogle Scholar
Yu, C., Teo, K. L., Zhang, L. and Bai, Y., “A new exact penalty function method for continuous inequality constrained optimization problems”, J. Ind. Manag. Optim. 6 (2010) 895–910; doi:10.3934/jimo.2010.6.895.Google Scholar
Zhu, M. and Martinez, S., “On distributed convex optimization under inequality and equality constraints”, IEEE Trans. Automat. Control 57 (2012) 151–164; doi:10.1109/tac.2011.2167817.Google Scholar