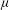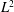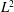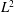Nanopore science, the study of individual nanoscale pores within thin membranes, is a fast-growing field which presents numerous interesting problems for physicists and applied mathematicians. Nanopores are most commonly applied to resistive pulse sensing (RPS) of individual particles suspended in aqueous electrolyte. The form of a resistive pulse is dependent on an array of experimental variables, including electrolyte characteristics, electrophoretic and convective transport, and (especially) pore and particle geometry. The level of analysis required depends on the application, but any broadly useful approach should be simple and flexible, due to the requirement for high data throughput and variations between different experimental systems and specimens. Here we review analytic methods for interpreting RPS experiments for particles in the approximate range 100 nm to 1 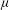 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu $m, focusing on calculation of resistance change as a function of the particle’s position. We detail a recently developed semi-analytical model and compare the modelled electric field with finite element results. The model can also be used to calculate particle motion, so that the experimental current–time history can be reconstructed. This approach is useful for a wide range of pore and particle geometries, and includes consideration of entrance effects. Tunable elastomeric pores with truncated linear cone geometry are used as a model system.
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mu $m, focusing on calculation of resistance change as a function of the particle’s position. We detail a recently developed semi-analytical model and compare the modelled electric field with finite element results. The model can also be used to calculate particle motion, so that the experimental current–time history can be reconstructed. This approach is useful for a wide range of pore and particle geometries, and includes consideration of entrance effects. Tunable elastomeric pores with truncated linear cone geometry are used as a model system.
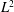 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}L^2$ ESTIMATES FOR THE SEMIDISCRETE GALERKIN METHOD APPLIED TO PARABOLIC INTEGRO-DIFFERENTIAL EQUATIONS WITH NONSMOOTH DATA