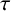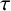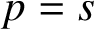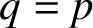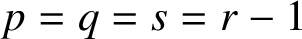Two simple mathematical models of advection and diffusion of hydrogen within the retina are discussed. The work is motivated by the hydrogen clearance technique, which is used to estimate blood flow in the retina. The first model assumes that the retina consists of three, well-mixed layers with different thickness, and the second is a two-dimensional model consisting of three regions that represent the layers in the retina. Diffusion between the layers and leakage through the outer edges are considered. Solutions to the governing equations are obtained by employing Fourier series and finite difference methods for the two models, respectively. The effect of important parameters on the hydrogen concentration is examined and discussed. The results contribute to understanding the dispersal of hydrogen in the retina and in particular the effect of flow in the vascular retina. It is shown that the predominant features of the process are captured by the simpler model.

We study a fractional-order delayed predator-prey model with Holling–Tanner-type functional response. Mainly, by choosing the delay time $\tau $ as the bifurcation parameter, we show that Hopf bifurcation can occur as the delay time $\tau $ passes some critical values. The local stability of a positive equilibrium and the existence of the Hopf bifurcations are established, and numerical simulations for justifying the theoretical analysis are also presented.

We develop a new analytical solution of a three-dimensional atmospheric pollutant dispersion. The main idea is to subdivide vertically the planetary boundary layer into sub-layers, where the wind speed and eddy diffusivity assume average values for each sub-layer. Basically, the model is assessed and validated using data obtained from the Copenhagen diffusion and Prairie Grass experiments. Our findings show that there is a good agreement between the predicted and observed crosswind-integrated concentrations. Moreover, the calculated statistical indices are within the range of acceptable model performance.

We consider two classes of irreducible Markovian arrival processes specified by the matrices C and D: the Markov-modulated Poisson process (MMPP) and the Markov-switched Poisson process (MSPP). The former exhibits a diagonal matrix D while the latter exhibits a diagonal matrix C. For these two classes we consider the following four statements: (I) the counting process is overdispersed; (II) the hazard rate of the event-stationary interarrival time is nonincreasing; (III) the squared coefficient of variation of the event-stationary process is greater than or equal to one; (IV) there is a stochastic order showing that the time-stationary interarrival time dominates the event-stationary interarrival time. For general MSPPs and order two MMPPs, we show that (I)–(IV) hold. Then for general MMPPs, it is easy to establish (I), while (II) is shown to be false by a counter-example. For general simple point processes, (III) follows from (IV). For MMPPs, we conjecture that (IV) and thus (III) hold. We also carry out some numerical experiments that fail to disprove this conjecture. Importantly, modelling folklore has often treated MMPPs as “bursty”, and implicitly assumed that (III) holds. However, to the best of our knowledge, proving this is still an open problem.

The paper deals with the construction of explicit Nordsieck second derivative general linear methods with s stages of order p with $p=s$ and high stage order $q=p$ with inherent Runge–Kutta or quadratic stability properties. Satisfying the order and stage order conditions together with inherent stability conditions leads to methods with some free parameters, which will be used to obtain methods with a large region of absolute stability. Examples of methods with r external stages and $p=q=s=r-1$ up to order five are given, and numerical experiments in a fixed stepsize environment are presented.