The problem of withdrawing water through a line sink from a region containing an homogeneous fluid beneath a free surface is considered. Assuming steady, irrotational flow of an ideal fluid, solutions with low Froude number containing a stagnation point on the free surface above the sink are sought using a series substitution method. The solutions are shown to exist for a value of the Froude number up to a critical value of about 1.4. No solutions of this type are found for Froude numbers greater than this value.

Variable structure systems with sliding modes have been widely discussed and used in many different fields of applications. The precise behaviour at a switching surface is complicated because there the system is non-analytic. The damped simple harmonic oscillator with a nonlinear variable structure is discretised and analysed in detail, revealing the occurrence and structure of pseudo-sliding modes which give insight to the corresponding sliding modes for the continuous system. Necessary and sufficient conditions are obtained and the analysis illustrated with graphs from numerical solutions.

Coplanar forced oscillations of a mechanical system such as a seismometer or a fluid in a tank are modelled by the coplanar motion of periodically forced, weakly damped pendulum. We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum driven by a periodic torque. Sinusoidal approximations previously obtained for downward and inverted oscillations at small values of the dimensionless driving amplitude ε are continued into numerical solutions at larger values of ε. Resonance curves and stability boundaries are presented for downward and inverted oscillations of periods T, 2T, and 4T, where T(≡ 2π/ω) is the dimensionless forcing period. The symmetry-breaking, period-doubling sequences of oscillatory motion are found to occur in bands on the (ω, ε) plane, with the amplitudes of stable oscillations in one band differing by multiples of about π from those in the other bands, a structure similar to that of energy levels in wave mechanics. The sinusoidal approximations for symmetric T-periodic oscillations prove to be surprisingly accurate at the larger values of ε, the banded structure being related to the periodicity of the J0 Bessel function.

The purpose of this paper is to study a stochastic model which assesses the effect of mutual interference on the searching efficiency in populations of insect parasites. By looking carefully at the assumptions which govern the model, I shall explain why the searching efficiency is of the same order as the total number, N, in the population, a conclusion which is consistent with the predictions of population biologists; previous studies have reached the conclusion that the efficiency is of order . The major results of the paper establish normal approximations for the distribution of the numbers of active parasites. These are valid at all stages of the process, in particular the non-equilibrium phase, where explicit analytic formulae for the state-probabilities are unavailable.

In oil reservoirs, the less-dense oil often lies over a layer of water. When pumping begins, the oil-water interface rises near the well, due to the suction pressures associated with the well. A boundary-integral formulation is used to predict the steady interface shape, when the oil well is approximated by a series of sources and sinks or a line sink, to simulate the actual geometry of the oil well. It is found that there is a critical pumping rate, above which the water enters the oil well. The critical interface shape is a cusp. Efforts to suppress the cone by using source/sink combinations are presented.

Sufficient conditions are established for all solutions of the linear system

to be oscillatory, where qij ∈(−∞, ∞), τij ∈ (0, ∞), i, j = 1, 2, …, n.

In this paper, we consider a class of optimal control problems involving inequality continuous-state constraints in which the control is piecewise smooth. The requirement for this type of control is more stringent than that for the control considered in standard optimal control problems in which the controls are usually taken as bounded measurable functions. In this paper, we shall show that this class of optimal control problems can easily be transformed into an equivalent class of combined optimal parameter selection and optimal control problems. We shall then use the control parametrisation technique to devise a computational algorithm for solving this equivalent dynamic optimisation problem. Furthermore, convergence analysis will be given to support this numerical approach. For illustration, two nontrivial optimal control problems involving transferring cargo via a container crane will be solved using the proposed approach.

We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum driven by horizontal, periodic forcing of the pivot with maximum acceleration εg and dimensionless frequency ω. Analytical solutions for symmetric oscillations at smaller values of ε are continued into numerical solutions at larger values of ε. A wide range of stable oscillatory solutions is described, including motion that is symmetric or asymmetric, downward or inverted, and at periods equal to the forcing period T ≡ 2π/ω or integral multiples thereof. Stable running oscillations with mean angular velocity pω/q, where p and q are integers, are investigated also. Stability boundaries are calculated for swinging oscillations of period T, 2T and 4T; 3T and 6T; and for running oscillations with mean angular velocity ω. The period-doubling cascades typically culminate in nearly periodic motion followed by chaotic motion or some independent periodic motion.

The problem of an anisotropic elastic slab containing two arbitrarily-oriented coplanar cracks in its interior is considered. Using a Fourier integral transform technique, we reduce the problem to a system of simultaneous finite-part singular integral equations which can be solved numerically. Once the integral equations are solved, relevant quantities such as the crack energy can be readily computed. Numerical results for specific examples are obtained.

Consider the nonlinear neutral equation

where pi(t), hi(t), gj(t), Q(t) Є C[t0, ∞), limt→∞hi(t) = ∞, limt→∞gj(t) = ∞ i Є Im = {1, 2, …, m}, j Є In = {1, 2, …, n}. We obtain a necessary and sufficient condition (2) for this equation to have a nonoscillatory solution x(t) with limt→∞ inf|x(t)| > 0 (Theorems 5 and 6) or to have a bounded nonoscillatory solution x(t) with limt→∞ inf|x(t)| > 0 (Theorem 7).

We consider the phase-locked solutions of the differential equation governing planar motion of a weakly damped pendulum forced by a prescribed, vertical acceleration εg sin ωt of its pivot, where ω and t are dimensionless, and the unit of time is the reciprocal of the natural frequency. Resonance curves and stability boundaries are presented for downward and inverted oscillations of periods T, 2T, 4T, …, where T (≡ 2π/ω) is the forcing period. Stable, downward oscillations are found to occur in distinct regions of the (ω, ε) plane, reminiscent of the regions of stability of the Mathieu equation (which describes the equivalent undamped, parametrically excited pendulum motion). The regions are dominated by oscillations of frequencies 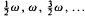, each region being bounded on one side by a vertical state at rest in stable equilibrium and on the other side by a symmetry-breaking, period-doubling sequence to chaotic motion. Stable, inverted oscillations are found to occur also in distinct regions of the (ω, ε) plane, the principal oscillation in each region being symmetric with period 2T.

This paper establishes some maximum and comparison principles relative to lower and upper solutions of nonlinear parabolic partial differential equations with impulsive effects. These principles are applied to obtain some sufficient conditions for the global asymptotic stability of a unique positive equilibrium in a reaction-diffusion equation modeling the growth of a single-species population subject to abrupt changes of certain important system parameters.

Wave reflection by a wedge in deep water is examined, where the wedge can represent a breakwater of finite length or the bow of a ship heading directly into the waves. In addition, the form of the solution allows the results to apply to ships heading at an angle into the waves. We consider a deep-water wavetrain approaching the wedge head on from infinity and being reflected. Far from the wedge there is a field of progressive waves (the incident wavetrain) while close to the wedge there is a short-crested wavefield (the incident and reflected wavetrains). A weakly-nonlinear slowly-varying averaged Lagrangian theory is used to describe the problem (see Whitham [16]) as the theory includes the nonlinear interaction between the incident and reflected wavetrains. This modelling of a short-crested wavefield allows the nonlinear wavefield to be found for broad wedges, as opposed to previous theories which are applicable to thin wedges only.

It is shown that the governing partial differential equations are hyperbolic and that the solution comprises two regions, within which the wave properties are constant separated by a wave jump. Given the wedge angle and the incident wavefield, the jump angle and the wave steepness and wavenumber of the short-crested wave-field behind the wave jump can be determined. Two solution branches are found to exist: one corresponds to regular reflection, while for small amplitudes the other is similar to Mach-reflection and so it is called near Mach-reflection. Results are presented describing both solution branches and the transition between them.

A uniform approximation to the description of a linear oscillator's slow resonant transition is calculated. If the time scale of the transition is ɛ−1, the approximation contains explicitly the 0(1) and 0(ɛ½) terms, and fixes a uniform 0(ɛ) error bound.

Centre manifolds arise in a rational approach to the problem of forming low-dimensional models of dynamical systems with many degrees of freedom. When a dynamical system with a centre manifold is subject to a small forcing, F, there are two effects: to displace the centre manifold; and to alter the evolution thereon. We propose a formal scheme for calculating the centre manifold of such a forced dynamical system. Our formalism permits the calculation of these effects, with errors of order |F|2. We find that the displacement of the manifold allows a reparameterisation of its description, and we describe two “natural” ways in which this can be carried out. We give three examples: an introductory example; a five-mode model of the atmosphere to display the quasi-geostrophic approximation; and the forced Kuramoto-Sivashinsky equation.

This paper is concerned with surface water waves produced by small oscillations of a thin vertical plate submerged in deep water. Green's integral theorem in the fluid region is used in a suitable manner to obtain the amplitude for the radiated waves at infinity. Particular results for roll and sway of the plate, and for a line source in the presence of a fixed vertical plate, are deduced.

Linear dynamical systems of the Rayleigh form are transformed by linear state variable transformations , where A and B are chosen to simplify analysis and reduce computing time. In particular, A is essentially a square root of M, and B is a Lyapunov quotient of C by A. Neither K nor C is required to be symmetric, nor is C small. The resulting state-space systems are analysed by factorisation of the evolution matrices into reducible factors. Eigenvectors and eigenvalues are determined by these factors. Conditions for further simplification are derived in terms of Kronecker determinants. These results are compared with classical reductions of Rayleigh, Duncan, and Caughey, which are reviewed at the outset.

We consider a generalised symmetric eigenvalue problem Ax = λMx, where A and M are real n by n symmetric matrices such that M is positive semidefinite. The purpose of this paper is to develop an algorithm based on the homotopy methods in [9, 11] to compute all eigenpairs, or a specified number of eigenvalues, in any part of the spectrum of the eigenvalue problem Ax = λMx. We obtain a special Kronecker structure of the pencil A − λM, and give an algorithm to compute the number of eigenvalues in a prescribed interval. With this information, we can locate the lost eigenpair by using the homotopy algorithm when multiple arrivals occur. The homotopy maintains the structures of the matrices A and M (if any), and the homotopy curves are n disjoint smooth curves. This method can be used to find all/some isolated eigenpairs for large sparse A and M on SIMD machines.

Using the fact that a differentiable quasi-convex function is also pseudo-convex at every point x of its domain where ∇f(x) ≠ 0 recent results relating different forms of convexity and invexity are strengthened.

An integral involving a combination of Legendre polynomials, exponential and algebraic terms is solved using the generating function. Special cases of this result are compared with known expansions, and the previously known results are shown to be extendible to a particularly pleasing result as a limiting case. Comparisons provide some new combinatorial identities involving binomials. Finally, an effective numerical procedure is described which evaluates the integral to machine accuracy.